Navigating a 3D Scene with Mouse and Keyboard
Reading time: 34 mins.In this lesson, we will explore how to navigate through 3D scenes using the mouse and keyboard, as illustrated in the video below, which features a screen recording from the Maya 3D tool. If you're unfamiliar with the term "navigating," think about your experience playing video games. For example, in third-person shooter games, you move through the game environment, typically using a joystick or the mouse and keyboard keys W, A, S, D. Essentially, this interaction is akin to moving through a 3D scene.
There's no need to dwell on why this skill is valuable. We're operating within a 3D, not 2D, context. Therefore, the reasons for wanting to move a 3D object or navigate through a 3D scene, such as a video game level, should be self-evident.
But how do we achieve this? That is the focus of this lesson.
As noted in the introduction, if you're accustomed to video games, you're likely familiar with navigating scenes using the W, A, S, D keys and the mouse, or possibly a joystick. For navigating our 3D scenes in this lesson, we will adopt the shortcut keys made popular by Maya, a practice many artists in the CG industry are familiar with. As you may be aware, if you've used different 3D software like Maya or Blender, each comes with its unique set of shortcut keys. Once accustomed to one software's shortcuts, switching to another can be challenging. In this lesson, we will utilize the same shortcut keys as Maya. However, customizing your set of keys, including implementing W, A, S, D, and mouse controls, could be an enjoyable exercise. This will become straightforward once you understand the underlying principles. Let's get started.
What Will We Achieve in this Lesson?
Explaining how to implement a 3D camera control system is straightforward. But there is a challenge and it lies in the fact that to demonstrate 3D camera controls in 3D scene in action, we need both a window and a way of rendering a 3D scene, ideally in real-time. Navigating through a 3D scene necessitates that we can render the scene as often as possible, ideally above 30 frames per second, which is considered the lower limit for a true real-time experience. Okay, that happens to not be so easy, because the ideal solution would be to use a real-time graphics 3D API such as Vulkan, DirectX, or Metal. The problem is that to render a basic triangle with Vulkan, you need to download some libraries (hopefully precompiled), link against them, and, more annoyingly, write about 2000 lines of code. That's not ideal.
So, what we will do instead is reuse the code from our previous lesson, where we learned how to create a window to display an image and draw on that image using the mouse. We'll use ray tracing to render our 3D scene. Instead of showing the static image of a lovely corgi, we will display the content of our ray-traced 3D scene. Now, this is easy since we have all the pieces of the puzzle. As mentioned before, we know how to display an image in a window, and we've learned that writing a naive ray-tracer is also straightforward. We covered this in section 1. Great! So we have everything we need to implement our 3D camera control system. The only "hiccup" is that ray tracing is slow (horribly slow), and without any optimization, even basic ones, we will be limited to rendering just a handful of triangles to stay within the 30 fps limit. But that's okay. A cube will do and is a good enough shape to demonstrate 3D navigation.
In this lesson, we will create a program, the workings of which are demonstrated in the screen recording provided in the video below. As usual, all the magic is contained within a single file, which you can compile using a single command line—no need for libraries, CMake, or any similar voodoo.
Let's Agree on Terminology
Generally, in the animation industry (and perhaps to a lesser extent in the video game industry), the type of camera model we're focusing on in this lesson is known as the free camera model. This contrasts with cameras whose motion in the scene follows a prerecorded path. When moving freely, you'll want to enable at least three types of motion:
-
Track: This is the ability to move sideways (left-right or up and down) with respect to the scene.
-
Dolly: This is the ability to get closer to or further from an object. It should not be confused with zooming. These are two different things. Dollying is like getting physically closer or further from an object. Zooming is staying where you are and changing the zoom on your camera to make the object appear bigger or smaller in frame. This is achieved by changing the camera's lens focal length.
-
Tumble (Rotate): This is akin to walking on a virtual sphere centered around the object that you are looking at.
While describing what rotating is, we've intuited two notions:
-
When you take a picture, you are generally aiming at some point. In CG, we often refer to this as the target.
-
When we suggested that you were walking on a virtual sphere centered around that "target" point (indeed), you inferred that the virtual sphere can vary in size. A larger sphere means you are farther from the object. A smaller sphere means you are closer to it. We call this the target distance. This is the distance between your camera and the target.
Great, we've introduced the key terms and concepts: dolly, track (also known as pan), tumble (rotate), target, and target distance.
We have illustrated these concepts in the following video.
Implementing Camera Controls in a 3D Environment.
Here is a detailed explanation.
Step 1: Identifying Camera Motion Triggers
This step's purpose is to determine when certain key and mouse combinations should initiate specific types of camera movement.
Initially, when we press the ALT key and/or move the mouse, we call a function that, in our code, will be OnMousePressed(). This function takes a parameter indicating the keys and mouse button that were pressed. If the combination of key and mouse should trigger one of the camera motions we discussed (track, dolly, tumble), then we set our free camera move type (CameraMoveType) to the correct type (which can be either TUMBLE, TRACK, or DOLLY):
struct FreeCameraModel {
enum class CameraMoveType : uint8_t {
NONE,
TUMBLE,
TRACK,
DOLLY,
};
FreeCameraModel() = default;
CameraMoveType move_type{CameraMoveType::NONE};
gfx::Point mouse_pos;
float theta{0};
float phi{0};
Vec3<float> look_at{0};
float distance_to_target{10};
Quat<float> camera_rotation;
};
FreeCameraModel freecam_model;
Matrix44<float> rotation_mat;
constexpr float kRotateAmplitude = 0.01;
constexpr float kPanAmplitude = 0.01;
constexpr float kScrollAmplitude = 0.1;
Matrix44<float> cam_to_world;
enum EventType {
ET_UNKNOWN = 0,
ET_MOUSE_PRESSED,
ET_MOUSE_RELEASED,
};
enum EventFlags {
EF_NONE = 0,
EF_SHIFT_DOWN = 1 << 0,
EF_CONTROL_DOWN = 1 << 1,
EF_ALT_DOWN = 1 << 2,
EF_LEFT_BUTTON_DOWN = 1 << 3,
EF_MIDDLE_BUTTON_DOWN = 1 << 4,
EF_RIGHT_BUTTON_DOWN = 1 << 5
};
void OnMousePressed(int flags, gfx::Point location) {
freecam_model.mouse_pos = location;
if (flags & EF_ALT_DOWN) {
freecam_model.move_type =
(flags & EF_LEFT_BUTTON_DOWN) ? FreeCameraModel::CameraMoveType::TUMBLE :
(flags & EF_MIDDLE_BUTTON_DOWN) ? FreeCameraModel::CameraMoveType::TRACK :
(flags & EF_RIGHT_BUTTON_DOWN) ? FreeCameraModel::CameraMoveType::DOLLY :
(assert(false), FreeCameraModel::CameraMoveType::NONE);
}
}
The context in which the OnMousePressed function is called will be discussed later, but for now, let's focus on what it does. It checks whether the mouse was pressed and whether the ALT key is also in the down state (pressed). Then, we look into which mouse button is being pressed: left, middle, or right. If it's the left button, then we set the camera's motion type to TUMBLE. For the middle and right mouse buttons, the camera move type will be set to TRACK and DOLLY, respectively. Dolly type is a bit special because, as we'll see later, we can also use the mouse wheel for that. So, that's the first step of the process. Depending on whether or not we have the right combination of keys and mouse, we set a flag (CameraMoveType move_type)indicating which type of motion we want to perform with the camera (which can be one of the three described).
Note that we also record the mouse position (freecam_model.mouse_pos = location;) when this function is called. This will be handy in step 2.
Step 2: Use the Mouse Differential Positions to Apply the Desired Effect
Differential positions refer to the change in the mouse's position from one moment to the next. This difference is crucial for calculating movements such as camera rotation, panning, or zooming in computer graphics applications. Essentially, it's the mouse's displacement that's used to determine how the camera should move or rotate in response to user input. It's worth noting that this technique is also used to move or rotate 3D objects, but that's a topic for another lesson.
When the mouse moves, we will call another function called OnMouseMoved(const gfx::Point& location). Note that the location parameter is nothing more than the mouse position at the time OnMouseMoved is called. The mouse coordinates are int, which is why they have their own gfx::Point class. Remember, we recorded the mouse position when the user pressed ALT +, say, the left mouse button (activating the TUMBLE move type). Then, in OnMouseMoved, we first calculate the difference (the deltas) between the previously recorded mouse position and the new one (passed to OnMouseMoved via the location parameter), as follows:
void OnMouseMoved(const gfx::Point& location) {
gfx::Point delta = location - freecam_model.mouse_pos;
freecam_model.mouse_pos = location;
...
}
After calculating the deltas, we update freecam_model.mouse_pos with the most recent mouse position. This will be used to calculate new deltas the next time OnMouseMoved is called, which will occur if the user continuously moves the mouse or pauses and starts moving it again while maintaining the ALT and left mouse button pressed.
These deltas are what will be used to calculate the amount of transformation to be applied to the camera to achieve the tumble, track, and dolly effects. If the user moves the mouse to the left, the new x- mouse position will be less than the previously recorded mouse position. Subtracting the old position from the new one results in a negative delta for x. We can apply this value to the translation of the camera's target along the x-axis, effectively moving the camera to the left (and the geometry seen through the camera to the right). In tumble mode, we use these deltas to increment or decrement the camera's rotation parameters, expressed in spherical coordinates, \(\theta\) and \(\phi\). So, doing something like theta += delta.x changes the rotation of the camera around the y-axis. With negative values, \(\theta\) decreases, rotating the camera about the y-axis clockwise, while with positive values, \(\theta\) increases, causing the camera to rotate counterclockwise. Same applies to \(\phi\) (using delta.y) which controls the camera elevation.
The application of these deltas to each move type will now be detailed. We'll first consider each type of motion individually and then see how to combine them into a final model. Before we start, remember that our default camera is initialized at the world origin, looking down the positive z-axis, as illustrated in Figure 1.

Note that the speed at which we want the camera to move in the scene, based on mouse motion, can vary according to personal preference. Whether you want your camera movement to be as swift as Speedy Gonzales or as leisurely as a lumbering giant, it's practical to adjust these values according to the scale of the scene. The essential goal is to have some control over the camera's movement speed. For this reason, each type of motion in the code/model has its specific amplitude parameter: kPanAmplitude, kScrollAmplitude, and kRotateAmplitude for tracking, dollying, and rotating move types, respectively (ideally, their names should align with the camera movement types — a nod to developer fatigue).
Tumble (Rotate)
Starting with tumble is a bit unusual, but the steps we are going to follow to calculate the final camera position start with knowing the camera's rotation, so we'll need it to proceed with the next two motion types. Okay, to create our free camera model, we are going to need both 4x4 matrices and quaternions. As far as matrices are concerned, Scratchapixel has many lessons devoted to them, starting with the Geometry lesson, so we assume this is covered. As for quaternions, we haven't written the lesson yet, and for many of you, quaternions might be a complete mystery. No panic! We've got you covered.
-
First, the sample code that comes with this lesson includes an implementation of all the methods we need for matrices, vectors, and quaternions to complete our demo. So, you won't have to deal with fancy and unknown libraries.
-
Second, the code related to quaternions won't be more than 100 lines. So, not a lot.
-
Thirdly, all you need to know about quaternions in the context of this lesson is that they are a kind of mathematical way to represent rotation around a given axis. All you need to create a quaternion is the axis around which you want to rotate and an angle by which you want something to be rotated by this quaternion. Simple.
Why quaternions? We could have put together a solution that relied solely on matrices. However, matrices suffer from a problem known as gimbal lock, which, in the context of 3D navigation, would manifest as sudden jumps in the camera's rotation. These jumps occur in specific cases, and since the lesson is not on gimbal lock and the limitations of matrices, we won't delve into more detail. It's important to know that quaternions do not suffer from this gimbal lock problem and therefore constitute a more stable and robust mathematical method for encoding rotations than matrices. That's why we are going to use them. Again, stay calm; how we are going to use them is really simple, and as for why and how they work, you'll just have to take the red pill for the time being.
Okay, as mentioned above, a rotation can be encoded in terms of spherical coordinates (as also explained in the lesson on geometry). With spherical coordinates, we can represent the rotation in terms of two angles (expressed in radians: \(\theta\) and \(\phi\)).
-
\(\theta\) (theta): Controls the elevation, the rotation around the x-axis.
-
\(\phi\) (phi): Controls the rotation around the y-axis, which you can refer to as the rotated object's azimuth. Think of it as a satellite spinning around the world's Equator.

Since our deltas contain two values, one accounting for the mouse motion along the screen's x-axis and one for the mouse motion along the y-axis, we will use these deltas, as previously calculated, to increment or decrement the \(\theta\) and \(\phi\) angles, respectively, depending on whether the delta values are positive or negative. Initially, both angles are set to 0, and the code proceeds as follows:
void OnMouseMoved(const gfx::Point& location) {
gfx::Point delta = location - freecam_model.mouse_pos;
freecam_model.mouse_pos = location;
if (freecam_model.move_type == FreeCameraModel::CameraMoveType::NONE)
return;
switch (freecam_model.move_type) {
case FreeCameraModel::CameraMoveType::TUMBLE: {
freecam_model.theta -= delta.x * kRotateAmplitude;
freecam_model.phi -= delta.y * kRotateAmplitude;
UpdateCameraRotation();
}
break;
case FreeCameraModel::CameraMoveType::DOLLY:
// ...
break;
case FreeCameraModel::CameraMoveType::TRACK:
// ...
break;
default:
break;
}
SetCameraMatrices();
}
In our case, we will subtract the delta value from the \(\theta\) angle because we are dealing with a right-handed coordinate system, and when the mouse goes up, the delta is negative whereas we want the elevation to increase, thus seeing \(\phi\) increase. Once we are done updating our spherical coordinate angles, we call a function UpdateCameraRotation, whose code follows:
void UpdateCameraRotation() {
Quat<float> q1; q1.SetAxisAngle(Vec3<float>(1,0,0), freecam_model.phi);
Quat<float> q2; q2.SetAxisAngle(Vec3<float>(0,1,0), freecam_model.theta);
freecam_model.camera_rotation = q2 * q1;
rotation_mat = freecam_model.camera_rotation.ToMatrix44();
}
We create two quaternions, one to rotate the camera by \(\phi\) along the x-axis and another by \(\theta\) along the y-axis. Multiplying the two quaternions together gives us another quaternion that encodes both rotations. All we have to do is convert this quaternion to a matrix by calling the ToMatrix44() method. Now, we have a matrix rotation_mat that encodes the camera's rotation. This rotation matrix will be used as we apply the dolly and track transformations.
We will delve into the SetCameraMatrices() function later, as we explore the dolly movement in more detail.
Dolly
Rotation is cool, but to effectively view the object, we need to create some distance from it. By default, the camera is positioned at the world's origin, which places it inside our cube. To achieve a better view, we must move the camera away from the origin along the direction it faces. In fact, we move it in the opposite direction of where the camera is currently looking. The camera's rotation plays a crucial role in this process. We start by rotating the vector (0,0,1) — the vector that points in the opposite direction to where the camera initially faces — using the camera's rotation matrix. This effectively aligns the vector in the direct opposite direction to where the camera is looking. Next, we move the camera from the target position along this vector to the desired distance. Elementary, Watson.
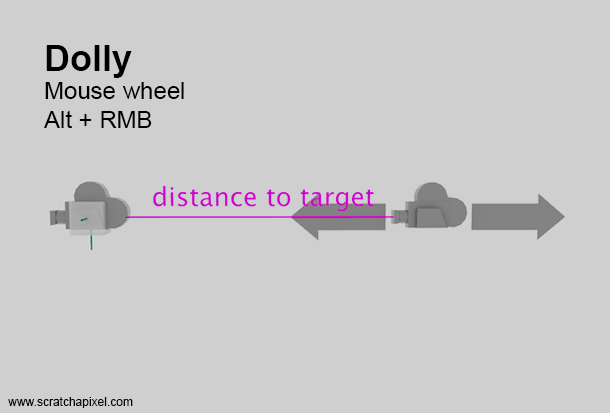
In Maya, moving closer to or further from the target is achieved by scrolling the middle mouse wheel. This can also be accomplished by pressing Alt and the right mouse button (MMB) simultaneously and moving the mouse left-right or up-down. Each rotation of the mouse wheel by one notch increments the target distance by a small amount. Depending on whether we scroll the wheel forward or backward, the increment will be either positive or negative, effectively allowing us to increase or decrease the distance to the target. This action moves the camera closer to or further from the target, which, for now, is centered in the middle of our 3D cube (at the world origin). Note that if we dolly using Alt+RMB rather than the wheel, the OnMouseMove function will be called instead of the OnMouseWheel function. However, note that internally within the OnMouseMove function, it is the OnMouseWheel function that is being invoked. We replace the mouse wheel delta obtained from rotating the wheel with the delta calculated from moving the mouse (where the final delta value is obtained by summing up delta.x and delta.y).
void OnMouseWheel(int scroll_amount) {
freecam_model.distance_to_target -= scroll_amount * kScrollAmplitude;
SetCameraMatrices();
}
void OnMouseMoved(const gfx::Point& location) {
gfx::Point delta = location - freecam_model.mouse_pos;
freecam_model.mouse_pos = location;
if (freecam_model.move_type == FreeCameraModel::CameraMoveType::NONE)
return;
switch (freecam_model.move_type) {
case FreeCameraModel::CameraMoveType::TUMBLE: {
...
}
break;
case FreeCameraModel::CameraMoveType::DOLLY:
OnMouseWheel(delta.x + delta.y);
return;
case FreeCameraModel::CameraMoveType::TRACK: {
...
}
break;
default:
break;
}
SetCameraMatrices();
}
Now this is where the SetCameraMatrices() comes into play.
void SetCameraMatrices() {
Vec3<float> camera_orient;
rotation_mat.MultDirMatrix(Vec3<float>(0,0,1), camera_orient);
Vec3<float> camera_position = freecam_model.look_at +
freecam_model.distance_to_target * camera_orient;
cam_to_world = rotation_mat;
cam_to_world[3][0] = camera_position.x;
cam_to_world[3][1] = camera_position.y;
cam_to_world[3][2] = camera_position.z;
}
This function updates the global cam_to_world matrix, encoding the camera's position and rotation using various parameters: target, rotation, and distance to the target. First, we multiply the vector (0,0,1) by the rotation_mat 4x4 matrix. Then, we calculate the final camera position as the target position plus the oriented vector, multiplied by the distance to the target ("distance from the target" might be more precise, but the concept should be clear). Consequently, we assign rotation_mat to the cam_to_world matrix to establish the camera's rotation. Afterward, we set the first three coefficients of the last row in the cam_to_world matrix with the x, y, and z coordinates of the camera position, respectively. In a row-major matrix, these three coefficients determine the translation necessary for any point to which the matrix is applied. We now have a complete cam_to_world matrix for transforming the camera ray origin (the translation part of the cam_to_world matrix) and ray direction (via the rotation part of the cam_to_world matrix), whether we are using ray-tracing or passing the matrix and its inverse to the vertex shader of our GPU rendering pipeline. For APIs such as Vulkan, Metal, DirectX, WebGL, and OpenGL (if still in use), it is in the vertex shader that vertices are transformed from world space to camera space, necessitating the inverse of cam_to_world.
Track
In Maya, tracking can be achieved by pressing alt and the right mouse button (RMB) simultaneously. Moving the mouse left causes the camera to move left, moving it right causes the camera to move right. Moving the mouse up causes the camera to ascend, while moving it down causes the camera to descend. In essence, the camera mimics the mouse's motion on the screen.

To grasp what tracking entails, envision a surface—imagine a sheet of paper—placed in the xy plane of the scene, effectively dividing the cube into front and back sections. To say it differently, this plane is perpendicular to the camera's viewpoint (see Figure 4), with the target point situated on that plane. Tracking can be thought of as if the target and the camera are linked by a bar, making the entire assembly rigid. As a result, moving the target causes the camera to move correspondingly, and vice versa (but in practice we will move the target).
float kTrackAmplitude = 0.1;
Vec3<float> target(0);
void OnMouseMoved(const gfx::Point& location) {
gfx::Point delta = location - freecam_model.mouse_pos;
freecam_model.mouse_pos = location;
...
switch (freecam_model.move_type) {
case FreeCameraModel::CameraMoveType::TUMBLE: {
...
}
break;
case FreeCameraModel::CameraMoveType::DOLLY:
...
break;
case FreeCameraModel::CameraMoveType::TRACK: {
Vec3<float> target_offset;
rotation_mat.MultDirMatrix(
Vec3<float>(-kPanAmplitude * delta.x, kPanAmplitude * delta.y, 0),
target_offset);
freecam_model.look_at += target_offset;
}
break;
default:
break;
}
SetCameraMatrices();
}
Code-wise, what we do is create a point on the xy plane representing the displacement of the target proportional to the mouse position deltas. Then, we rotate that point to account for the camera rotation. Think of it as rotating the plane in which the point lies, with the plane remaining perpendicular to the camera direction. Then, we apply this small offset to the current target position. This is equivalent to moving the target point within the plane that is perpendicular to the camera's aiming direction. In the case of tracking, the displacement is calculated based on mouse movement deltas as if the displacement were occurring from the origin. This displacement vector is then rotated according to the current camera orientation. This approach ensures that the displacement reflects how you would move the target in the camera's view, irrespective of the target's initial position. The way the code is structured allows for the initial target position to be set to any value, and the resulting operation will still be accurate.
Note that for both tumble and track movements, we need to invoke SetCameraMatrices() to update our global cam_to_world matrix. For the dolly movement, this update occurs within the OnMouseWheel function.
Final Code Listing
Remember that all the code samples from Scratchapixel are available on GitHub.
That's it, pixel friends. You've just learned how to implement a 3D camera and control its motion using your mouse and keyboard. We've been using the same shortcuts as those used in Maya. Video gamers and Blender users are encouraged to implement their own controls, ensuring you feel just at home. Here is the full source code of the program that is not longer than 600 lines. Quite remarkable, yes, considering that it includes, without using any external libraries, the required code for vectors, matrices, and quaternions as well as the ray-tracing code.
Note that, by the way, most of the vector, quaternion, and matrix class code is inspired by the Imath library, which is open-source and was initially designed by the VFX studio ILM. Feel free to download this library, which, for once, is not hard to compile, and replace our code with it as an exercise if you wish.
Also, note how in our code we apply the cam_to_world matrix that we updated as we applied the various camera motion types to transform the primary ray direction, effectively providing the illusion that we are moving through the scene. We are just rendering a simple cube here, as rendering anything more than 12 triangles without any optimization with ray-tracing would lead, on our 3.6GHz processor (single core), to a framerate lower than 30 fps, but feel free to experiment with your own geometry.
As for the Windows-related code, we have explained most of it in the lesson on creating your own window to display an image and draw on top of it. The principles are the same here, except that we've adapted them to our specific problems at hand. That involves tracking the keys being pressed and when the left, middle, and right mouse buttons are pressed or released, which then triggers the call to the OnMousePressed, OnMouseMoved, and OnMouseWheel functions. This process is pretty straightforward and relates more to the Windows API than to the 3D camera control implementation itself.
To compile:
clang++ -std=c++23 -Wall -Wextra -luser32 -lgdi32 -o 3d-nav-controls.exe 3d-nav-controls.cc -O3
Using the -O3 optimization flag is crucial in this context. Since ray-tracing can be slow, you need to ensure your code runs as fast as possible. Utilizing this optimization flag will ensure that the code is optimized to the fullest extent of the compiler's capabilities, allowing the resulting code to run as efficiently as possible.
Final note: There are different ways of implementing 3D camera controls, but this one is rather common and works perfectly fine. If you want to suggest different approaches or methods, or highlight some errors in this lesson, don't hesitate to reach out to us on Discord.
As usual, if this lesson was beneficial to you and if you learned or use what you learned here in your own code, if you can afford it, make a donation to Scratchapixel so we can keep bringing more content to people and get rewarded for our effort, which is to bring professional-grade content for free to the community (consider what you would pay a school or for a book to acquire this knowledge through traditional avenues. We pay because it represents the time and knowledge of individuals). If you can't afford a few bucks (because you are just starting out or facing challenges in life), we understand. A quick thank you on our Discord will do. So, let us know how you are doing and show us the cool stuff you are creating with this content.
// (c) scratchapixel - 2024
// Distributed under the terms of the CC BY-NC-ND 4.0 License.
// https://creativecommons.org/licenses/by-nc-nd/4.0/
// clang++ -std=c++23 -Wall -Wextra -std=c++23 -luser32 -lgdi32 -o 3d-nav-controls.exe 3d-nav-controls.cc -O3
#define _USE_MATH_DEFINES
#include <cmath>
#include <cstdint>
#include <cassert>
#include <iostream>
namespace gfx {
struct Point {
int x, y;
constexpr Point() : x(0), y(0) {}
constexpr Point(int x, int y) : x(x), y(y) {}
constexpr Point operator-(const Point& pt) const {
return Point(x - pt.x, y - pt.y);
}
};
}
template<typename T>
class Vec3 {
public:
Vec3() : x(T(0)), y(T(0)), z(T(0)) {}
Vec3(T xx) : x(T(xx)), y(T(xx)), z(T(xx)) {}
Vec3(T xx, T yy, T zz) : x(T(xx)), y(T(yy)), z(T(zz)) {}
constexpr Vec3<T> Normalized() const {
T l = std::sqrt(x * x + y * y + z * z);
if (l == 0) [[unlikely]] return Vec3(T(0));
return Vec3(x / l, y / l, z / l);
}
constexpr Vec3<T>& Normalize() {
T l = std::sqrt(x * x + y * y + z * z);
if (l != 0) [[likely]] {
x /= l;
y /= l;
z /= l;
}
return *this;
}
constexpr T Dot(const Vec3<T>& v) const {
return x * v.x + y * v.y + z * v.z;
}
constexpr T operator^ (const Vec3<T>& v) const {
return Dot(v);
}
constexpr Vec3<T> Cross(const Vec3<T>& v) const {
return Vec3(
y * v.z - z * v.y,
z * v.x - x * v.z,
x * v.y - y * v.x);
}
constexpr Vec3<T> operator%(const Vec3<T>& v) const {
return Cross(v);
}
constexpr Vec3<T> operator*(T r) const {
return Vec3<T>(x * r, y * r, z * r);
}
friend constexpr Vec3<T> operator*(T r, const Vec3<T>& v) {
return Vec3<T>(v.x * r, v.y * r, v.z * r);
}
constexpr Vec3<T> operator-(const Vec3<T>& v) const {
return Vec3<T>(x - v.x, y - v.y, z - v.z);
}
constexpr Vec3<T> operator+(const Vec3<T>& v) const {
return Vec3<T>(x + v.x, y + v.y, z + v.z);
}
constexpr Vec3<T>& operator+=(const Vec3<T>& v) {
x += v.x, y += v.y, z += v.z;
return *this;
}
friend std::ostream& operator<<(std::ostream& os, const Vec3<T>& v) {
return os << v.x << " " << v.y << " " << v.z;
}
T x, y, z;
};
template<typename T>
class Matrix44 {
public:
Matrix44() {
x[0][0] = 1; x[0][1] = 0; x[0][2] = 0; x[0][3] = 0;
x[1][0] = 0; x[1][1] = 1; x[1][2] = 0; x[1][3] = 0;
x[2][0] = 0; x[2][1] = 0; x[2][2] = 1; x[2][3] = 0;
x[3][0] = 0; x[3][1] = 0; x[3][2] = 0; x[3][3] = 1;
}
constexpr Matrix44 (
T a, T b, T c, T d,
T e, T f, T g, T h,
T i, T j, T k, T l,
T m, T n, T o, T p) {
x[0][0] = a; x[0][1] = b; x[0][2] = c; x[0][3] = d;
x[1][0] = e; x[1][1] = f; x[1][2] = g; x[1][3] = h;
x[2][0] = i; x[2][1] = j; x[2][2] = k; x[2][3] = l;
x[3][0] = m; x[3][1] = n; x[3][2] = o; x[3][3] = p;
}
constexpr T* operator[](size_t i) {
return x[i];
}
constexpr const T* operator[](size_t i) const {
return x[i];
}
constexpr void MultVecMatrix(const Vec3<T>& src, Vec3<T>& dst) const {
T a, b, c, w;
a = src.x * x[0][0] + src.y * x[1][0] + src.z * x[2][0] + x[3][0];
b = src.x * x[0][1] + src.y * x[1][1] + src.z * x[2][1] + x[3][1];
c = src.x * x[0][2] + src.y * x[1][2] + src.z * x[2][2] + x[3][2];
w = src.x * x[0][3] + src.y * x[1][3] + src.z * x[2][3] + x[3][3];
dst.x = a / w;
dst.y = b / w;
dst.z = c / w;
}
constexpr void MultDirMatrix(const Vec3<T>& src, Vec3<T>& dst) const {
T a, b, c;
a = src.x * x[0][0] + src.y * x[1][0] + src.z * x[2][0];
b = src.x * x[0][1] + src.y * x[1][1] + src.z * x[2][1];
c = src.x * x[0][2] + src.y * x[1][2] + src.z * x[2][2];
dst.x = a, dst.y = b, dst.z = c;
}
T x[4][4];
};
template<typename T>
class Quat {
public:
Quat() = default;
constexpr Quat(T s, T i, T j, T k)
: r(s), v(i, j, k) {
}
constexpr Quat(T s, Vec3<T> d)
: r(s), v(d) {
}
constexpr Quat<T>& SetAxisAngle(const Vec3<T>& axis, T radians) {
v = axis.Normalized() * std::sin(radians / 2);
r = std::cos(radians / 2);
return *this;
}
constexpr Matrix44<T> ToMatrix44() const {
return Matrix44<T>(
1 - 2 * (v.y * v.y + v.z * v.z),
2 * (v.x * v.y + v.z * r),
2 * (v.z * v.x - v.y * r),
0,
2 * (v.x * v.y - v.z * r),
1 - 2 * (v.z * v.z + v.x * v.x),
2 * (v.y * v.z + v.x * r),
0,
2 * (v.z * v.x + v.y * r),
2 * (v.y * v.z - v.x * r),
1 - 2 * (v.y * v.y + v.x * v.x),
0,
0,
0,
0,
1);
}
T r{1}; // The real part
Vec3<T> v{0,0,0}; // The imaginary vector
};
// Quaternion multiplication
template<typename T>
constexpr inline Quat<T> operator* (const Quat<T>& q1, const Quat<T>& q2) {
return Quat<T>(
q1.r * q2.r - (q1.v ^ q2.v), q1.r * q2.v + q1.v * q2.r + q1.v % q2.v);
}
struct FreeCameraModel {
enum class CameraMoveType : uint8_t {
NONE,
TUMBLE,
TRACK,
DOLLY,
};
FreeCameraModel() = default;
CameraMoveType move_type{CameraMoveType::NONE};
gfx::Point mouse_pos;
float theta{0};
float phi{0};
Vec3<float> look_at{0};
float distance_to_target{10};
Quat<float> camera_rotation;
};
FreeCameraModel freecam_model;
Matrix44<float> rotation_mat;
constexpr float kRotateAmplitude = 0.01;
constexpr float kPanAmplitude = 0.01;
constexpr float kScrollAmplitude = 0.1;
Matrix44<float> cam_to_world;
const Vec3<float> points[8] = {
{-0.5, -0.5, 0.5},
{ 0.5, -0.5, 0.5},
{-0.5, 0.5, 0.5},
{ 0.5, 0.5, 0.5},
{-0.5, 0.5, -0.5},
{ 0.5, 0.5, -0.5},
{-0.5, -0.5, -0.5},
{ 0.5, -0.5, -0.5},
};
const uint32_t tri_vertex_indices[36] = {
0, 1, 2, 2, 1, 3, 2, 3, 4,
4, 3, 5, 4, 5, 6, 6, 5, 7,
6, 7, 0, 0, 7, 1, 1, 7, 3,
3, 7, 5, 6, 0, 4, 4, 0, 2
};
enum EventType {
ET_UNKNOWN = 0,
ET_MOUSE_PRESSED,
ET_MOUSE_RELEASED,
};
enum EventFlags {
EF_NONE = 0,
EF_SHIFT_DOWN = 1 << 0,
EF_CONTROL_DOWN = 1 << 1,
EF_ALT_DOWN = 1 << 2,
EF_LEFT_BUTTON_DOWN = 1 << 3,
EF_MIDDLE_BUTTON_DOWN = 1 << 4,
EF_RIGHT_BUTTON_DOWN = 1 << 5
};
void OnMousePressed(int flags, gfx::Point location) {
freecam_model.mouse_pos = location;
if (flags & EF_ALT_DOWN) {
freecam_model.move_type =
(flags & EF_LEFT_BUTTON_DOWN) ? FreeCameraModel::CameraMoveType::TUMBLE :
(flags & EF_MIDDLE_BUTTON_DOWN) ? FreeCameraModel::CameraMoveType::TRACK :
(flags & EF_RIGHT_BUTTON_DOWN) ? FreeCameraModel::CameraMoveType::DOLLY :
(assert(false), FreeCameraModel::CameraMoveType::NONE);
}
}
void OnMouseReleased() {
freecam_model.move_type = FreeCameraModel::CameraMoveType::NONE;
}
void UpdateCameraRotation() {
Quat<float> q1; q1.SetAxisAngle(Vec3<float>(1,0,0), freecam_model.phi);
Quat<float> q2; q2.SetAxisAngle(Vec3<float>(0,1,0), freecam_model.theta);
freecam_model.camera_rotation = q2 * q1;
rotation_mat = freecam_model.camera_rotation.ToMatrix44();
}
void SetCameraMatrices() {
Vec3<float> camera_orient;
rotation_mat.MultDirMatrix(Vec3<float>(0,0,1), camera_orient);
Vec3<float> camera_position = freecam_model.look_at +
freecam_model.distance_to_target * camera_orient;
cam_to_world = rotation_mat;
cam_to_world[3][0] = camera_position.x;
cam_to_world[3][1] = camera_position.y;
cam_to_world[3][2] = camera_position.z;
}
void OnMouseWheel(int scroll_amount) {
freecam_model.distance_to_target -= scroll_amount * kScrollAmplitude;
SetCameraMatrices();
}
void OnMouseMoved(const gfx::Point& location) {
gfx::Point delta = location - freecam_model.mouse_pos;
freecam_model.mouse_pos = location;
if (freecam_model.move_type == FreeCameraModel::CameraMoveType::NONE)
return;
switch (freecam_model.move_type) {
case FreeCameraModel::CameraMoveType::TUMBLE: {
freecam_model.theta -= delta.x * kRotateAmplitude;
freecam_model.phi -= delta.y * kRotateAmplitude;
UpdateCameraRotation();
} break;
case FreeCameraModel::CameraMoveType::DOLLY:
OnMouseWheel(delta.x + delta.y);
return;
case FreeCameraModel::CameraMoveType::TRACK: {
Vec3<float> target_offset;
rotation_mat.MultDirMatrix(
Vec3<float>(-kPanAmplitude * delta.x, kPanAmplitude * delta.y, 0),
target_offset);
freecam_model.look_at += target_offset;
}
break;
default:
break;
}
SetCameraMatrices();
}
// Rendering
#include <chrono>
#include <fstream>
constexpr uint32_t width = 640;
constexpr uint32_t height = 480;
constexpr float super_far = 1.e6;
float angle = 50.f;
#define UNICODE
#define NOMINMAX
#include <windows.h>
#include <windowsx.h> // GET_X_LPARAM
const wchar_t* CLASSNAME = L"myapp_window";
HWND hwnd;
HDC hdcBuffer;
void* pvBits; // Pointer to the bitmap's pixel bits
HBITMAP hbmBuffer;
template<typename T>
T DegreesToRadians(const T& degrees) {
return M_PI * degrees / T(180);
}
struct Hit {
float t{super_far};
float u, v;
Vec3<float> Ng;
};
inline float Xorf(const float x, const float y) {
std::uint32_t ix, iy;
std::memcpy(&ix, &x, sizeof(float));
std::memcpy(&iy, &y, sizeof(float));
std::uint32_t resultInt = ix ^ iy;
float result;
std::memcpy(&result, &resultInt, sizeof(float));
return result;
}
void Intersect(const Vec3<float>& ray_orig,
const Vec3<float>& ray_dir,
const Vec3<float>& p0,
const Vec3<float>& p1,
const Vec3<float>& p2,
Hit& hit) {
const float ray_near = 0.1;
const Vec3<float> e1 = p0 - p1;
const Vec3<float> e2 = p2 - p0;
const Vec3<float> Ng = e1.Cross(e2);
const Vec3<float> C = p0 - ray_orig;
const Vec3<float> R = ray_dir.Cross(C);
const float det = Ng.Dot(ray_dir);
const float abs_det = std::abs(det);
const float sign_det = std::copysign(0.f, det);
if (det == 0) [[unlikely]] return;
const float U = Xorf(R.Dot(e2), sign_det);
if (U < 0) [[likely]] return;
const float V = Xorf(R.Dot(e1), sign_det);
if (V < 0) [[likely]] return;
const float W = abs_det - U - V;
if (W < 0) [[likely]] return;
const float T = Xorf(Ng.Dot(C), sign_det);
if (T < abs_det * ray_near || abs_det * hit.t < T) [[unlikely]] return;
const float rcp_abs_det = 1.f / abs_det;
hit.u = U * rcp_abs_det;
hit.v = V * rcp_abs_det;
hit.t = T * rcp_abs_det;
hit.Ng = Ng.Normalized();
}
float fps;
void Render() {
auto start = std::chrono::steady_clock::now();
float aspect_ratio = width / static_cast<float>(height);
float scale = std::tan(DegreesToRadians(0.5f * angle));
Vec3<float> ray_orig;
cam_to_world.MultVecMatrix(Vec3<float>(0,0,0), ray_orig);
char* pixel = (char*)pvBits;
memset(pixel, 0x0, width * height * 3);
for (uint32_t j = 0; j < height; ++j) {
float y = (1 - 2 * (j + 0.5f) / static_cast<float>(height)) * scale * 1 / aspect_ratio;
for (uint32_t i = 0; i < width; ++i) {
float x = (2 * (i + 0.5f) / static_cast<float>(width) - 1) * scale;
Vec3<float> ray_dir(x, y, -1);
ray_dir.Normalize();
cam_to_world.MultDirMatrix(ray_dir, ray_dir);
float t = super_far;
for (size_t n = 0, ni = 0; n < 12; n++, ni += 3) {
Hit hit;
const Vec3<float>& v0 = points[tri_vertex_indices[ni]];
const Vec3<float>& v1 = points[tri_vertex_indices[ni + 1]];
const Vec3<float>& v2 = points[tri_vertex_indices[ni + 2]];
Intersect(ray_orig, ray_dir, v0, v1, v2, hit);
if (hit.t < t) {
t = hit.t;
char color = static_cast<char>(255 * std::max(0.f, ray_dir.Dot(hit.Ng)));
pixel[(i + j * width) * 3] =
pixel[(i + j * width) * 3 + 1 ] =
pixel[(i + j * width) * 3 + 2 ] = color;
}
}
}
}
auto end = std::chrono::steady_clock::now();
fps = 1000.f / std::chrono::duration_cast<std::chrono::milliseconds>(end - start).count();
InvalidateRect(hwnd, NULL, TRUE);
UpdateWindow(hwnd);
}
// Windows related stuff
LRESULT CALLBACK WndProc(HWND hWnd, UINT msg, WPARAM wParam, LPARAM lParam) {
switch(msg) {
case WM_CLOSE:
DeleteObject(hbmBuffer);
DestroyWindow(hWnd);
break;
case WM_CREATE:
//Render();
break;
case WM_DESTROY:
PostQuitMessage(0);
break;
case WM_LBUTTONUP:
case WM_MBUTTONUP:
case WM_RBUTTONUP:
OnMouseReleased();
break;
case WM_LBUTTONDOWN:
case WM_MBUTTONDOWN:
case WM_RBUTTONDOWN: {
gfx::Point location(GET_X_LPARAM(lParam), GET_Y_LPARAM(lParam));
unsigned int flags = 0;
if (GetKeyState(VK_SHIFT) & 0x8000) flags |= EF_SHIFT_DOWN;
if (GetKeyState(VK_CONTROL) & 0x8000) flags |= EF_CONTROL_DOWN;
if (GetKeyState(VK_MENU) & 0x8000) flags |= EF_ALT_DOWN; // VK_MENU is the Alt key
if (wParam & MK_LBUTTON) flags |= EF_LEFT_BUTTON_DOWN;
if (wParam & MK_MBUTTON) flags |= EF_MIDDLE_BUTTON_DOWN;
if (wParam & MK_RBUTTON) flags |= EF_RIGHT_BUTTON_DOWN;
OnMousePressed(flags, location);
Render();
}
break;
case WM_MOUSEMOVE: {
int xpos = GET_X_LPARAM(lParam);
int ypos = GET_Y_LPARAM(lParam);
OnMouseMoved(gfx::Point(xpos, ypos));
Render();
}
break;
case WM_MOUSEWHEEL: {
int delta = GET_WHEEL_DELTA_WPARAM(wParam) / WHEEL_DELTA;
OnMouseWheel(delta);
Render();
}
break;
case WM_ERASEBKGND:
return 1; // Indicate that background erase is handled
case WM_PAINT: {
PAINTSTRUCT ps;
HDC hdcWindow = BeginPaint(hwnd, &ps);
BitBlt(hdcWindow, 0, 0, width, height, hdcBuffer, 0, 0, SRCCOPY);
std::wstring text = L"fps: " + std::to_wstring(fps);
SetTextColor(hdcWindow, RGB(255, 255, 255)); // White text
SetBkMode(hdcWindow, TRANSPARENT);
TextOut(hdcWindow, 10, 10, text.c_str(), text.length());
} break;
default:
return DefWindowProc(hWnd, msg, wParam, lParam);
}
return 0;
}
void CreateAndRegisterWindow(HINSTANCE hInstance) {
WNDCLASSEX wc = {};
wc.cbSize = sizeof(WNDCLASSEX);
wc.lpfnWndProc = WndProc;
wc.hInstance = hInstance;
wc.lpszClassName = CLASSNAME;
wc.hCursor = LoadCursor(nullptr, IDC_ARROW); // Set the default arrow cursor
wc.hIcon = LoadIcon(hInstance, IDI_APPLICATION); // Load the default application icon
wc.hbrBackground = (HBRUSH)(COLOR_WINDOW + 1);
wc.lpszMenuName = nullptr;
wc.hIconSm = LoadIcon(hInstance, IDI_APPLICATION); // Load the small icon for the application
if (!RegisterClassEx(&wc)) {
MessageBox(nullptr, L"Window Registration Failed", L"Error",
MB_ICONEXCLAMATION | MB_OK);
}
hwnd = CreateWindowEx(
WS_EX_CLIENTEDGE,
CLASSNAME,
L"3D Navigation Controls",
WS_OVERLAPPEDWINDOW & ~WS_THICKFRAME & ~WS_MAXIMIZEBOX, // non-resizable
CW_USEDEFAULT, CW_USEDEFAULT, width, height,
nullptr, nullptr, hInstance, nullptr);
if (hwnd == nullptr) {
MessageBox(nullptr, L"Window Creation Failed", L"Error",
MB_ICONEXCLAMATION | MB_OK);
}
HDC hdcScreen = GetDC(hwnd); // Obtain the screen/device context
hdcBuffer = CreateCompatibleDC(hdcScreen); // Create a compatible device context for off-screen drawing
BITMAPINFO bmi;
ZeroMemory(&bmi, sizeof(bmi)); // Ensure the structure is initially empty
bmi.bmiHeader.biSize = sizeof(BITMAPINFOHEADER);
bmi.bmiHeader.biWidth = width; // Specify the width of the bitmap
bmi.bmiHeader.biHeight = -height; // Negative height for a top-down DIB
bmi.bmiHeader.biPlanes = 1;
bmi.bmiHeader.biBitCount = 24; // 24 bits per pixel (RGB)
bmi.bmiHeader.biCompression = BI_RGB; // No compression
hbmBuffer = CreateDIBSection(hdcBuffer, &bmi, DIB_RGB_COLORS, &pvBits, NULL, 0);
SelectObject(hdcBuffer, hbmBuffer);
ReleaseDC(hwnd, hdcScreen);
ShowWindow(hwnd, SW_SHOWDEFAULT); // or use WS_VISIBLE but more control with this option
Render();
}
int main() {
HINSTANCE hInstance = GetModuleHandle(NULL);
freecam_model.look_at = Vec3<float>(0); //points[0];
UpdateCameraRotation();
SetCameraMatrices();
CreateAndRegisterWindow(hInstance);
MSG msg;
while (1) {
while(PeekMessage(&msg, nullptr, 0, 0, PM_REMOVE) != 0) {
TranslateMessage(&msg);
DispatchMessage(&msg);
if (msg.message == WM_QUIT) {
break;
}
}
if (msg.message == WM_QUIT)
break;
}
return 0;
}