Ray-Tracing: Rendering a Triangle

Barycentric Coordinates

Reading time: 23 mins.

Barycentric Coordinates

Barycentric coordinates are particularly important in computer graphics. They serve several functions and are key to the ray-triangle intersection algorithm proposed by Möller-Trumbore, which will be studied in the next chapter. How barycentric coordinates are used in computer graphics (outside of the ray-triangle intersection context) will also be discussed at the end of this chapter. So, read this section carefully, as you will encounter this concept quite frequently.

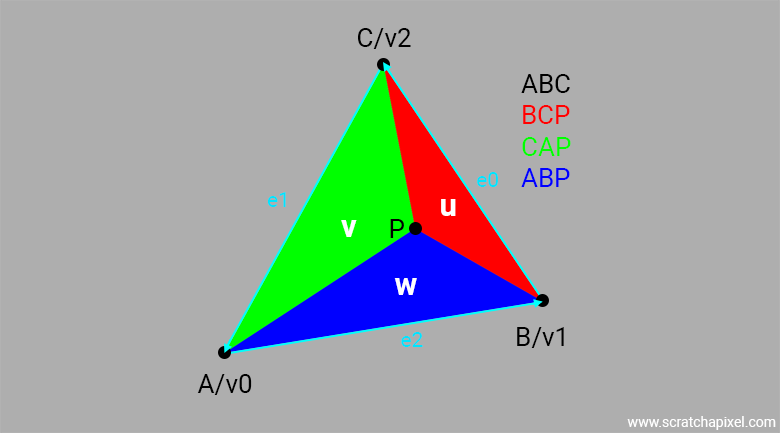
Barycentric coordinates allow us to express the position of any point located on a triangle using three scalars. This includes any position inside the triangle, any position on one of the triangle’s edges, or at one of its vertices. To compute the position of this point using barycentric coordinates, we use the following equation:

$$P = uA + vB + wC$$

where A (often denoted as $v0$ in code), B ($v1$), and C ($v2$) are the vertices of the triangle, and $u$, $v$, and $w$ are the barycentric coordinates. These coordinates are real numbers (scalars, or floats/doubles in programming terms), and they have the unique property of being normalized such that:

$$u + v + w = 1$$

Because of this normalization property, note that if you know two of the coordinates, you can determine the third. For instance: $w = 1 - u - v$, which also implies $u + v \leq 1$ (we will use this simple but important property later on).

Equation 1 defines the position of point P on the plane of the triangle formed by the vertices A, B, and C. The point is within the triangle (A, B, C) if $0 \leq u, v, w \leq 1$. If any one of the coordinates is less than zero or greater than one, the point is outside the triangle. If any of the coordinates is zero, P lies on one of the edges of the triangle.

You can also simply use two coordinates (let's say u and v) to express the coordinates of P in a two-dimensional coordinate system defined by its origin (A) and the edge AB and AC (pretty much like expressing 2D points in the orthogonal two-dimensional coordinate system defined by an x- and y-axis. The only difference in our case is that AB and AC are not necessarily orthogonal and that the origin of this coordinate system is A). Anyway, just to say that you can define a position inside the triangle with the equation $P = A + u*AB + v*AC$ (where $u \ge 0$ and $v \ge 0$ and $u + v \le 1$). This equation can read as, "starts from A, move a little bit in the direction of AB, then a little bit in the direction of AC and you will find P". Now if you develop this equation you can write:

$$ \begin{array}{l} P = A + u(B - A) + v(C - A) = \\ A + uB - uA + vC - vA = (1 - u - v) * A + u * B + v * C \end{array} $$

This equation is similar to equation 1 except that if $w = 1 - u - v$ you have the following formula:

$$P = w * A + u * B + v * C$$

instead of

$$P = u * A + v * B + w * C.$$

These two equations are mathematically equivalent, but it’s not immediately clear why we often write $(1 - u - v) * A + u * B + v * C$ instead of $u * A + v * B + (1 - u - v) * C$ without the explanation we've just provided. In the initial version of this lesson, this explanation was just a footnote, but I’ve since promoted it to an important note because, as you examine code or read papers that use barycentric coordinates, you may encounter authors who assign the $u$, $v$, and $w$ coordinates in different ways.

For example, you might come across formulations like $wA + uB + vC$ or $uA + wB + vC$, among others. The specific arrangement doesn’t matter as long as two conditions hold: first, the normalization property $u + v + w = 1$ must be satisfied, and second, all the barycentric coordinates must be greater than or equal to zero. Of course, you cannot assign the coefficients $u$, $v$, and $w$ to any vertex randomly. Each coefficient must be assigned to a specific vertex, and the pairing depends on how you calculate these coefficients. The way you compute the coordinates determines which barycentric coordinate you "pair" with each vertex of the triangle. We will explore this pairing in the code later.

For simplicity and consistency throughout this lesson, we will always assume the pairing $uA + vB + wC$. All calculations in this lesson will use this pairing, which will determine how we calculate $u$, $v$, and $w$.

More specifically, one reason why our choice of pairing might not be the default in some cases is that it implies edge0 is the edge defined by points $B$ and $C$ (see Figure 1), whereas the more intuitive approach might be to consider edge0 as the edge defined by points $A$ and $B$. Therefore, be mindful of the "pairing" your code is using, as it will depend on which edge you are using to calculate $u$ and $v$. If you are using different edges to calculate $u$ and $v$ than we are, make sure to adapt the code that interpolates $P$ accordingly. The result should be the same in the end, which is ultimately what matters. With this important note in mind, let's proceed.

Barycentric coordinates are also known as areal coordinates. Although not very commonly used, this term indicates that the coordinates u, v, and w are proportional to the area of the three sub-triangles defined by P, the point located on the triangle, and the triangle's vertices (A, B, C). These three sub-triangles are denoted ABP, BCP, and CAP (see Figure 1).

This leads us to the formulas used to compute the barycentric coordinates:

$$ \begin{array}{l} u = {\dfrac{TriangleBCP_{Area}}{TriangleABC_{Area}}}\\ v = {\dfrac{TriangleCAP_{Area}}{TriangleABC_{Area}}}\\ w = {\dfrac{TriangleABP_{Area}}{TriangleABC_{Area}}}\\ \end{array} $$

In the rest of this lesson, we will assume that $u$ is associated with the triangle $\triangle BCP$, $v$ with the triangle $\triangle CAP$, and $w$ with the triangle $\triangle ABP$. As mentioned in the important note above, there is no strict convention regarding how you pair the barycentric coordinate letters to these three sub-triangles defined by the larger triangle $\triangle ABC$ and a point $P$ lying on that triangle. Therefore, as you explore the source code of different projects using barycentric coordinates, you might encounter a variety of combinations.

As also noted earlier, while perhaps not as common (though used in some production renderers we've had the chance to review), we will consistently stick to the pairing: $u \rightarrow \triangle BCP$, $v \rightarrow \triangle CAP$, and $w \rightarrow \triangle ABP$.

**Figure 2:** to compute the area of a triangle we start from the formula used to compute a parallelogram (its base multiplied by its height H). To compute H, we multiply sin($\theta$) by the length of the vector AC.

Computing the area of a triangle is straightforward. If you duplicate the triangle and mirror it along its longest edge, you get a parallelogram. To compute the area of the parallelogram, simply multiply its base by its height, scaled by $\sin(\theta)$, where $\theta$ is the angle subtended by the vectors AB and AC (see Figure 2). Since the parallelogram consists of two triangles, the area of one triangle is half the area of the parallelogram.

With this understanding, computing $u$ and $v$ becomes easy (with $w$ determined from $u$ and $v$ as explained earlier).

$$ \text{Area of the Triangle} = \frac{{||B - A|| \cdot ||C - A|| \cdot \sin(\theta)}}{2} $$

This formula calculates the area of a triangle using the lengths of vectors $B - A$ and $C - A$, with $\theta$ representing the angle between these two vectors. The area is half of the parallelogram formed by these vectors.

To simplify things, we can take advantage of the fact that the areas of the sub-triangles $ \triangle BCP$, $ \triangle CAP$, and $ \triangle ABP$ are proportional to the magnitudes of the cross products we computed in the previous chapter to find $P$, the intersection point. One of the key properties of the cross product is that its magnitude represents the area of the parallelogram formed by the two vectors.

Therefore, we don’t need to explicitly compute the previous formula (which involves the "expensive" $\sin(\theta)$). Instead, we can use the following:

$$ \begin{aligned} \text{Parallelogram Area} &= ||(B - A) \times (C - A)|| \\ \text{Triangle Area} &= \frac{\text{Parallelogram Area}}{2} \end{aligned} $$

This approach again allows us to bypass the need for trigonometric functions, simplifying the computation. Note that, in mathematical terms, the double bars notation ($|| ||$) represents the "length" or magnitude of a vector. In other words, we need to compute the length of the vector resulting from the cross product $(B - A) \times (C - A)$. Since we already know how to compute both the cross product of two vectors and the length of a vector, we now have everything we need to calculate the barycentric coordinates of the intersection point.

bool rayTriangleIntersect(
    const Vec3f& orig, const Vec3f& dir,
    const Vec3f& v0, const Vec3f& v1, const Vec3f& v2,
	const Vec3f& P,
    float& t, float& u, float& v)
{
	// compute plane's normal
    Vec3f v0v1 = v1 - v0;
    Vec3f v0v2 = v2 - v0;
    // no need to normalize
    Vec3f N = v0v1.crossProduct(v0v2); // N

    // Ray-plane intersection: solving t from the plane equation
    float NdotRayDirection = N.dotProduct(dir);
    if (fabs(NdotRayDirection) < 1e-8) return false; // Ray is parallel to the triangle

    float d = N.dotProduct(v0); // Plane constant
    t = (N.dotProduct(v0) - N.dotProduct(orig)) / NdotRayDirection;

    // If t is negative, the triangle is behind the ray
    if (t < 0) return false; 

    // Compute the intersection point P
    Vec3f P = orig + dir * t;

    // Step 2: Calculate area of the triangle
    float area = N.length() / 2; // Area of the full triangle

    // Step 3: Inside-outside test using barycentric coordinates
	Vec3f C;

    // Calculate u (for triangle BCP)
    Vec3f v1p = P - v1;
	Vec3f v1v2 = v2 - v1;
    C = v1v2.crossProduct(v1p);
    u = (C.length() / 2) / area;
    if (N.dotProduct(C) < 0) return false; // P is on the wrong side

    // Calculate v (for triangle CAP)
    Vec3f v2p = P - v2;
    Vec3f v2v0 = v0 - v2;
    C = v2v0.crossProduct(v2p);
    v = (C.length() / 2) / area;
    if (N.dotProduct(C) < 0) return false; // P is on the wrong side

    // Third edge
    Vec3f v0p = P - v0;
	// Vec3f v0v1 = v1 - v0; -> already defined
    C = v0v1.crossProduct(v0p);
    if (N.dotProduct(C) < 0) return false; // P is on the right side

    // The point is inside the triangle
    return true;
}

Note that for this code to work, the plane normal is not normalized because we use the vector's length to compute the triangle's area.

Using Barycentric Coordinates

Barycentric coordinates are especially useful in shading. A triangle is a flat surface, and we can associate additional information or data (such as points, colors, vectors, etc.) to each of its vertices. This extra data is typically referred to as vertex data or vertex attributes. For example, imagine assigning the color red to vertex A, green to vertex B, and blue to vertex C.

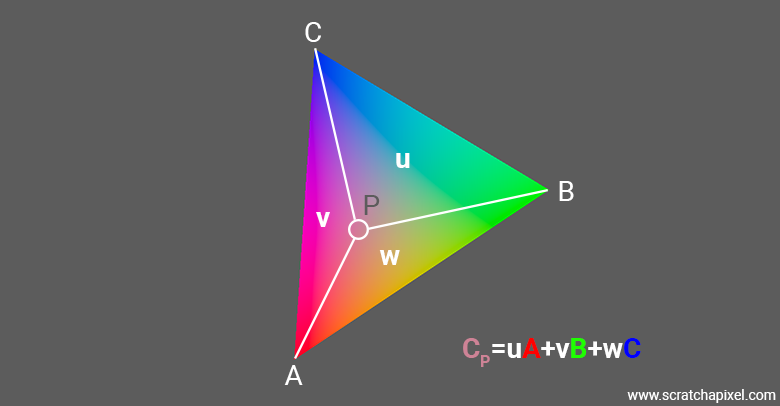
**Figure 3:** barycentric coordinates can be used to interpolate vertex data at the hit point. In this example, for example, we compute the color at P using vertex color.

If the intersection point coincides with one of the triangle's vertices, the color of the object at that point is simply the color associated with that vertex—simple enough. The question is, what happens when the ray intersects the triangle anywhere else (either on an edge or inside the triangle)? When barycentric coordinates are used to compute the position of a point on the triangle based on the triangle’s vertices, we can interpolate any other data defined at the vertices (such as color) in the same way. In other words, barycentric coordinates are used to interpolate vertex data (or attributes) across the triangle’s surface. This technique can be applied to any data type, such as floats, colors, etc.

This interpolation method is particularly useful for shading, where it can be used to interpolate the normal at the intersection point. Normals of an object can be defined on a per-face or per-vertex basis (referred to as face normals or vertex normals, respectively). If normals are defined per vertex, we can use this interpolation technique to simulate smooth shading across the triangle's surface, even though the triangle itself is geometrically flat. The normal at the hit point is a combination of the vertex normals, so if the vertex normals differ from each other, the result of this interpolation will vary across the surface, producing a smooth-shading effect.

// vertex position
Vec3f triVertex[3] = {{-3,-3,5}, {0,3,5}, {3,-3,5}};
// vertex data
Vec3f triColor[3] = {{1,0,0}, {0,1,0}, {0,0,1}};
if (rayTriangleIntersect(...)) {
    // Compute pixel color
    // col = u * col0 + v * col1 + w * col2 with w = 1 - u - v
    Vec3f ColorPhit = u * triColor[0] + v * triColor[1] + (1 - u - v) * triColor[2];
}

Barycentric coordinates are also used to compute texture coordinates (we will study this topic in the lesson on texturing).

Optimizing The Computation Of Barycentric Coordinates

We use the cross product between $BC$ and $BP$, as well as between $CA$ and $CP$, to compute $u$ and $v$, respectively. However, if you look at the code again, you'll notice that we've already computed these cross products for the inside-outside test. They were used to determine whether point $P$ is on the right or left side of the edges $BC$ and $CA$. Naturally, the first optimization is to reuse the results of these calculations. Also, notice that (see Equation 2):

$$ \begin{array}{l} u & = & \dfrac{triangleBCP_{area}}{triangleABC_{area}} \\ & = & \dfrac{parallelogramBCP_{area} / 2}{parallelogramABC_{area} / 2} = \dfrac{parallelogramBCP_{area}}{parallelogramABC_{area}} = \dfrac{||BC \times BP||}{||AB \times AC||} \end{array} $$

There is no need to compute the triangle area explicitly since the ratio between the triangle $BCP$ and the triangle $ABC$ is the same as the ratio between the parallelogram $BCP$ (which is twice the area of the triangle $BCP$) and the parallelogram $ABC$ (which is twice the area of the triangle $ABC$). Therefore, we can also avoid the division by 2. The code becomes:

bool rayTriangleIntersect(
    const Vec3f &orig, const Vec3f &dir,
    const Vec3f &v0, const Vec3f &v1, const Vec3f &v2,
    float &t, float &u, float &v)
{
	// compute plane's normal
	Vec3f v0v1 = v1 - v0;
    Vec3f v0v2 = v2 - v0;
    // no need to normalize
    Vec3f N = v0v1.crossProduct(v0v2); // N
    float area2 = N.length();
 
    // Step 1: finding P
    
    // check if the ray and plane are parallel.
    float NdotRayDirection = N.dotProduct(dir);
    if (fabs(NdotRayDirection) < kEpsilon) // almost 0
        return false; // they are parallel so they don't intersect! 

    // compute d parameter using equation 2
    float d = -N.dotProduct(v0);
    
    // compute t (equation 3)
    t = -(N.dotProduct(orig) + d) / NdotRayDirection;
    // check if the triangle is behind the ray
    if (t < 0) return false; // the triangle is behind
 
    // compute the intersection point using equation 1
    Vec3f P = orig + t * dir;
 
    // Step 2: inside-outside test
    Vec3f C; // vector perpendicular to the triangle's plane
 
	// Calculate u (for triangle BCP)
	Vec3f v1p = P - v1;
	Vec3f v1v2 = v2 - v1;
    Vec3f C = v1v2.crossProduct(v1p);
	u = C.length() / area2;
    if (N.dotProduct(C) < 0) return false; // P is on the right side
 
    // Calculate v (for triangle CAP)
    ...

    return true; // this ray hits the triangle
}

Finally, we can prove that (Equation 3):

$$ u = {\dfrac{triangleBCP_{area}} {triangleABC_{area}}} = {\dfrac{(BC \times BP) \cdot N}{(AB \times AC) \cdot N}} $$

First, remember that $N = AB \times AC$. Therefore, we can rewrite the above formula as:

$$ u = {\dfrac{triangleBCP_{area}}{triangleABC_{area}}} = {\dfrac{(BC \times BP) \cdot N}{N \cdot N}} $$

We now need to prove that this equation is true. Recall from the lesson on geometry that the dot product of two vectors can be interpreted as:

$$||A|| \cdot ||B|| = \cos(\theta) ||A|| ||B||$$

where the angle $\theta$ is the angle subtended by the two vectors $A$ and $B$, and $||A||$ and $||B||$ are the magnitudes of vectors $A$ and $B$, respectively. We also know that when two vectors $A$ and $B$ are collinear (pointing in the same direction), the angle between them is 0, so $\cos(0) = 1$. The result of $N \cdot N$ (the dot product of a vector with itself) is $\cos(0)||N|| ||N|| = ||N||^2$, which is the square of the vector $N$'s magnitude.

Now, let's consider the numerator in Equation 3. From the construction (because the points $A$, $B$, $C$, and $P$ are coplanar), the triangles $BCP$ and $ABC$ are coplanar. Therefore, the vectors resulting from the cross products $BC \times BP$ and $AB \times AC$ are also collinear (pointing in the same direction). We can rewrite the numerator as:

$$\textcolor{blue}{(BC \times BP) \cdot N} = \textcolor{green}{(BC \times BP)} \cdot \textcolor{red}{(AB \times AC)}$$

Let’s define $\textcolor{green}{BC \times BP = A}$ and $\textcolor{red}{AB \times AC = N = B}$. Then:

$$\textcolor{blue}{(BC \times BP) \cdot N} = \cos(0) ||A|| ||B|| = ||A|| ||B||$$

In this case, $A$ and $B$ are collinear because they are constructed from coplanar vectors. Finally, we can substitute our results for the numerator and denominator in Equation 3:

$$u = \dfrac{triangleBCP_{area}}{triangleABC_{area}} = \dfrac{||BC \times BP|| \cdot N}{N \cdot N} = \dfrac{||A|| ||B||}{||B|| ||B||}$$

We can cancel out one of the $||B||$ terms, leaving us with:

$$u = \dfrac{triangleBCP_{area}}{triangleABC_{area}} = \dfrac{||A||}{||B||}$$

Substituting $A$ back with $\textcolor{green}{BC \times BP}$ and $B$ with $\textcolor{red}{AB \times AC}$, we get:

$$\dfrac{||A||}{||B||} = \dfrac{||BC \times BP||}{||AB \times AC||}$$

This equation is similar to the one we originally used to compute $u$ (Equation 2). Therefore, Equation 3 is also a valid formula for computing $u$. Since we already compute the numerator $(BC \times BP) \cdot N$ during the inside-outside test, we can reuse this result for the computation of the barycentric coordinates (a similar technique can be used for $v$).

In mathematics, the formula $(A \times B) \cdot C$ is called a scalar triple product (because it is the product of three vectors). It can be interpreted as the volume of a parallelepiped whose sides are defined by the vectors $A$, $B$, and $C$. It can also be understood as the determinant of a 3x3 matrix with these vectors as its rows, a property we will use in the next chapter.

Here’s the final version of our intersection routine, incorporating the optimized method for computing barycentric coordinates:

bool rayTriangleIntersect(
    const Vec3f &orig, const Vec3f &dir,
    const Vec3f &v0, const Vec3f &v1, const Vec3f &v2,
    float &t, float &u, float &v)
{
    // compute plane's normal
    Vec3f v0v1 = v1 - v0;
    Vec3f v0v2 = v2 - v0;
    // no need to normalize
    Vec3f N = v0v1.crossProduct(v0v2); // N
    float denom = N.dotProduct(N);

    // Step 1: finding P

    // check if ray and plane are parallel ?
    float NdotRayDirection = N.dotProduct(dir);

    if (fabs(NdotRayDirection) < kEpsilon) // almost 0
        return false; // they are parallel so they don't intersect !

    // compute d parameter using equation 2
    float d = -N.dotProduct(v0);

    // compute t (equation 3)
    t = -(N.dotProduct(orig) + d) / NdotRayDirection;

    // check if the triangle is in behind the ray
    if (t < 0) return false; // the triangle is behind

    // compute the intersection point using equation 1
    Vec3f P = orig + t * dir;

    // Step 2: inside-outside test
    Vec3f C; // vector perpendicular to triangle's plane

	// Calculate u (for triangle BCP)
    Vec3f v1p = P - v1;
	Vec3f v1v2 = v2 - v1;
    C = v1v2.crossProduct(v1p);
	if ((u = N.dotProduct(C)) < 0) return false; // P is on the right side

    // Calculate v (for triangle CAP)
    Vec3f v2p = P - v2;
	Vec3f v2v0 = v0 - v2;
    C = v2v0.crossProduct(v2p);
    if ((v = N.dotProduct(C)) < 0) return false; // P is on the right side

    Vec3f v0p = P - v0;
    C = v0v1.crossProduct(v0p);
    if (N.dotProduct(C) < 0) return false; // P is on the right side

    u /= denom;
    v /= denom;

    return true; // this ray hits the triangle
}

Source Code

In this version of the ray-triangle intersection method, we have implemented the technique described in chapter 3 to compute the hit point coordinates and the method described in this chapter to compute the barycentric coordinates of the intersected point. When a ray hits the triangle, you can choose between interpolating three colors using the barycentric coordinates or visualizing the raw coordinates directly.

...
constexpr float kEpsilon = 1e-8;

inline
float deg2rad(const float °)
{ return deg * M_PI / 180; }

inline
float clamp(const float &lo, const float &hi, const float &v)
{ return std::max(lo, std::min(hi, v)); }

bool rayTriangleIntersect(
    const Vec3f &orig, const Vec3f &dir,
    const Vec3f &v0, const Vec3f &v1, const Vec3f &v2,
    float &t, float &u, float &v)
{
     // compute plane's normal
    Vec3f v0v1 = v1 - v0;
    Vec3f v0v2 = v2 - v0;
    // no need to normalize
    Vec3f N = v0v1.crossProduct(v0v2); // N
    float denom = N.dotProduct(N);

    // Step 1: finding P

    // check if ray and plane are parallel ?
    float NdotRayDirection = N.dotProduct(dir);

    if (fabs(NdotRayDirection) < kEpsilon) // almost 0
        return false; // they are parallel so they don't intersect !

    // compute d parameter using equation 2
    float d = -N.dotProduct(v0);

    // compute t (equation 3)
    t = -(N.dotProduct(orig) + d) / NdotRayDirection;

    // check if the triangle is in behind the ray
    if (t < 0) return false; // the triangle is behind

    // compute the intersection point using equation 1
    Vec3f P = orig + t * dir;

    // Step 2: inside-outside test
    Vec3f C; // vector perpendicular to triangle's plane

	// Calculate u (for triangle BCP)
    Vec3f v1p = P - v1;
	Vec3f v1v2 = v2 - v1;
    C = v1v2.crossProduct(v1p);
	if ((u = N.dotProduct(C)) < 0) return false; // P is on the right side

    // Calculate v (for triangle CAP)
    Vec3f v2p = P - v2;
	Vec3f v2v0 = v0 - v2;
    C = v2v0.crossProduct(v2p);
    if ((v = N.dotProduct(C)) < 0) return false; // P is on the right side

    Vec3f v0p = P - v0;
    C = v0v1.crossProduct(v0p);
    if (N.dotProduct(C) < 0) return false; // P is on the right side

    u /= denom;
    v /= denom;

    return true; // this ray hits the triangle
}

int main(int argc, char **argv)
{
    Vec3f v0(-1, -1, -5);
    Vec3f v1( 1, -1, -5);
    Vec3f v2( 0,  1, -5);
    
    const uint32_t width = 640;
    const uint32_t height = 480;
	// v0 is yellow, v1 is cyan and v2 is magenta
    Vec3f cols[3] = {{1.f, 1.f, 0.f}, {0, 1.f, 1.f}, {1.f, 0.f, 1.f}};
    Vec3f *framebuffer = new Vec3f[width * height];
    Vec3f *pix = framebuffer;
    float fov = 51.52;
    float scale = tan(deg2rad(fov * 0.5));
    float imageAspectRatio = width / (float)height;
    Vec3f orig(0);
    for (uint32_t j = 0; j < height; ++j) {
        for (uint32_t i = 0; i < width; ++i) {
            // Compute primary ray
            float x = (2 * (i + 0.5) / (float)width - 1) * imageAspectRatio * scale;
            float y = (1 - 2 * (j + 0.5) / (float)height) * scale;
            Vec3f dir(x, y, -1);
            //cameraToWorld.multDirMatrix(Vec3f(x, y, -1), dir);
            dir.normalize();
            float t, u, v;
            if (rayTriangleIntersect(orig, dir, v0, v1, v2, t, u, v)) {
                *pix = u * cols[0] + v * cols[1] + (1 - u - v) * cols[2];
                //*pix = Vec3f(u, v, 1 - u - v); // To visualize u, v, w
            }
            pix++;
        }
    }
    
    // Save the result to a PPM image (keep these flags if you are on Windows)
    ...

    return 0;
}

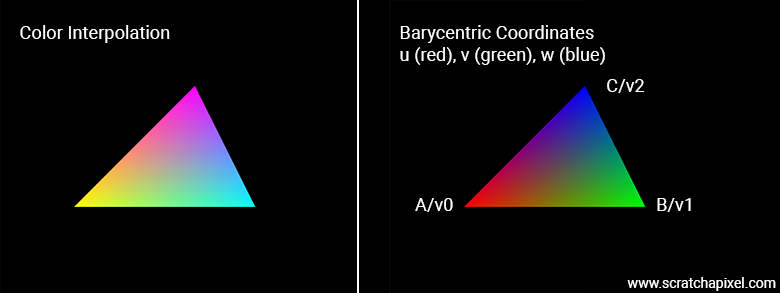
The image below shows the outputs of the program (you can find the source code in the last chapter of this lesson).

Trivia and a Bit of History

For fun, in 2024, I stumbled upon the infamous RTNews archive, which most readers may not know much about unless they were adults in the 80s and 90s. This was a kind of public forum where people interested in ray tracing would present and exchange ideas. Here is a copy of one such thread I found, specifically devoted to the calculation of Barycentric coordinates (here is the link to it):

From: hpfcla!bogart%gr@cs.utah.edu (Rod G. Bogart)
...
Another way to think of barycentric coordinates is by the relative areas of the subtriangles defined by the intersection point and the triangle vertices.

        1         If the area of triangle 123 is A, then the area of
       /|\        P23 is rA.  Area 12P is sA and area 1P3 is tA.
      / | \       With this image, it is obvious that r+s+t must equal
     /  |  \      one.  If r, s, or t go outside the range zero to one,
    / t | s \     P will be outside the triangle.
   /  _-P-_  \
  / _-     -_ \
 /_-    r    -_\
2---------------3
By using the above area relationships, the following equations define r, s, and t.

        N = triangle normal = (vec(1 2) cross vec(1 3))
            (vec(1 P) cross vec(1 3)) dot N
        s = -------------------------------
                     (length N)^2
            (vec(1 2) cross vec(1 P)) dot N
        t = -------------------------------
                     (length N)^2
        r = 1 - (s + t)

By the way, I love the use of ASCII for laying out the text, which was very common back then. Most of what’s in there should now be familiar to you. I’ve added this bit to both pay tribute to our peers and to provide some historical context about this topic, as well as to educate you on important historical facts related to computer graphics (which, in my opinion, is also important to learn about).