Generating Camera Rays with Ray-Tracing

Definition of a Ray

Prerequisites

Most of the techniques we will be studying from that lesson onwards will use what we learned about points, vectors, matrices, cameras, and trigonometry in the lesson on Geometry. We will reuse a lot of the things we learned in the lesson Computing the Pixel of a 3D Point about the different coordinates systems vertices and vectors can be transformed into. You should also be familiar with the concepts studied in the lesson 3D Viewing: the Pinhole Camera Model. Be sure you have covered these grounds first before you start reading this lesson.

What Is This Lesson About?

In the introductory lesson on Ray-Tracing, we already quickly mentioned how ray-tracing can be used to solve the visibility problem. Let's recall that visible surface determination in the context of 3D rendering is the process used to determine which parts of the scene geometry are visible through the camera. We can use ray tracing to compute visibility (this process was already explained in the previous lesson) by casting a ray through each pixel in the image and looking for the nearest object that this ray intersects (if any). Let's also recall that ray tracing is a technique for computing intersections between rays and surfaces. Using ray-tracing to compute visibility is also called ray-casting.

Given a set of obstacles in the Euclidean space, two points in the space are said to be visible to each other if the line segment that joins them does not intersect any obstacles - definition of [visibility](http://en.wikipedia.org/wiki/Visibility_(geometry)) on Wikipedia.

Producing an image using ray tracing to solve visibility requires looping over all the pixels in the image, generating a ray for each pixel, casting this ray into the scene, and looking for a possible intersection between this ray and any surface in the scene. These rays are called primary rays (or camera or eye rays) because they are the first rays cast into the scene (secondary rays are used to compute things like shadows, reflections, refractions, etc.). To find if the ray intersects a surface, we need to test each object in the scene for a possible intersection against this ray. A ray might intersect more than one surface. The visible surface is the surface with the closest intersection distance. By distance, we mean the distance from the origin of the ray (which in the case of a primary ray, is the position of the camera) and the intersection point.

for (int j = 0; j < height; ++j) { 
    for (int i = 0; i < width; ++i) { 
        // generate primary ray (this is what this lesson is about)
        ... 
        float tnear = INFINITY;  //closest intersection, set to INFINITY to start with 
        for (int k = 0; k < numObjects; ++k) { 
             float t = INFINITY;  //intersection to the current object if any 
             if objects[k]->intersect(pimaryRay, tnear) && t < tnear) { 
                 tnear = t; 
                 framebuffer= objects[k].color; 
            } 
        } 
    } 
} 

In this lesson, we will formalize the concept of ray and more importantly how primary rays are generated to simulate pinhole cameras. Once we understand how primary rays are generated, the next step will consist of learning a few techniques to compute the intersection between rays and geometry. These are the minimum requirements to produce an image of 3D objects using ray tracing.

In this chapter, we will learn a few useful things about rays. In the next chapter, we will study how primary rays are computed.

Defining Rays

As stated in the previous lesson,

Ray-tracing is a technique used to compute the visibility between points. It is simply a technique based on the concept of a ray which can be mathematically (and in a computer program) defined as a point (the origin of the ray in space) and a direction. Then the idea behind ray tracing is to find mathematical solutions to compute the intersection of this ray with various types of geometry: triangles, quadrics (which we study in one of the following lessons), NURBs, etc. This is all there is to ray tracing.

The part we will explain in this lesson (and in this chapter more specifically) is the notion of ray and the way we can define it both in theory and in programming. The only two variables we need to define a ray are a point and a vector. The point (which programmatically we will simply define as a vec3f represents the origin of the ray and the vector, its direction. Keep in mind that direction should generally be normalized.

// the minimum requirement for defining a ray is a position and a direction
Vec3f orig;  //ray origin 
Vec3f dir;  //ray direction (normalized) 

What this point and this direction represent when combined is a half-line. Mathematically, any point on this half-line can be defined as:

Where \(t\) is the distance from the origin of the point to the point on the half-line. This variable can either be negative or positive. It \(t\) is negative, the point on the ray is behind the ray origin and if \(t\) is positive, the point P is in "front" of the ray's origin. Practically, when we use ray tracing, we are generally only interested in finding the intersection of the ray with surfaces located in front of the ray's origin. This means that we will only consider an intersection between a ray and a surface valid if \(t\) is positive.

// define ray's origin and direction
Vec3f orig = ...; 
Vec3f dir = ...; 
float t = INFINITY; 
// does this ray intersect the object? intersect() returns true if an intersection was found
if (object.intersect(orig, dir, t) && t > 0) { 
    // this is a valid intersection, the hit point is in front of the ray's origin
    ... 
} 

From a mathematical standpoint, the equation above is called a parametric equation. The half-line is described by an equation which is a function of the parametric variable \(t\) (or parameter).

Ray-geometry intersection routines always return the intersection (if one was found) in terms of the parameter \(t\). In other words, if an intersection was found then the ray-geometry intersection routine would compute the distance from the ray origin to that intersection and return this information to you. From there you can easily compute the position of the intersection or hit point in 3D space using the ray parametric equation we introduced above.

// define ray's origin and direction
Vec3f orig = ...; 
Vec3f dir = ...; 
float t = INFINITY;  //intersection distance to the object (if any). Set to a very large number to start with 
// does this ray intersect the object? intersect() returns true if an intersection was found
if (object.intersect(orig, dir, t) && t > 0) { 
    // this is a valid intersection, the hit point is in front of the ray's origin, compute the hit point using t
    Vec3f hitPoint = orig + dir * t; 
} 

This is all there is to rays. From a programming point of view, rays can also be defined as a C++ class:

class Ray 
{ 
public: 
    Ray(), orig(0), dir(0,0,-1) {} 
    Ray(const Vec3f &o, const Vec3f &d) : orig(o), dir(d) {} 
    // etc.
    ... 
    Vec3f orig; 
    Vec3f dir; 
}; 

Some programmers like to add more member variables to this class, such as a \(t_{min}\) and a \(t_{max}\) distance. They define a range of valid values for \(t\). In other words, if the ray-geometry routine returns a value for \(t\) that is not contained within the range [\(t_{min}\), \(t_{max}\)], then there would be no intersection (even if \(t\) is greater than 0).

class Ray 
{ 
public: 
    Ray(), orig(0), dir(0,0,-1), tMin(0.1), tMax(1000) {} 
    Ray(const Vec3f &o, const Vec3f &d) : orig(o), dir(d), tMin(0.1), tMax(1000) {} 
    // etc.
    ... 
    Vec3f orig; 
    Vec3f dir; 
    float tMin, tMax; 
}; 
 
Ray ray; 
// set ray direction and origin
ray.orig = ...; 
ray.dir = ...; 
float t = INFINITY; 
if (object.intersect(ray, t) && t >= ray.tMin && t <= r.tMax) { 
     // valid intersection
     ... 
} 

You can add as many parameters as you want to the Ray class. You can decide whether to use a Ray class or not. This is entirely left to personal preferences and requirements. There is no rule about the way you represent this data in your program. Some programmers like to add information to the Ray class such as the distance \(t\) to the closest visible surface (which you set in the ray-geometry routine when an intersection is found), a pointer to the hit object, etc. Some other programmers prefer to separate this information from the ray variables and store them instead in a structure or a class called Intersection for instance. Again, apart from having to at least define the ray origin and ray direction, everything else can be done in just the way you like (and is optional).

What Are Rays Used For?

Rays can be used pretty much everywhere. They are used to solve the visibility problem, gather information about the colors of objects, compute shadows, etc. The type of rays we will be learning about in this lesson is called camera rays or primary rays.

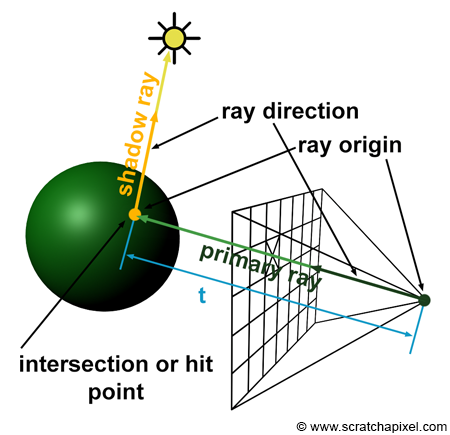
For each pixel in the frame, we will need to construct one camera ray which we will cast into the scene. If rays intersect objects we will compute the color of the objects at these intersection points and assign these colors to the corresponding pixels. This is in short, how a CG image is created with ray tracing. We can make the distinction between primary rays (the first rays cast into the scene which have for origin the origin of the camera) and secondary rays (shadow, diffuse, specular, transmission, etc. rays) which we use in shading. Secondary rays are spawned from primary rays at the ray's intersection point. The direction of these secondary rays depends on their type: shadow (we cast a ray in the direction of the light), reflection (we cast a ray in the reflection direction), refraction (we cast a ray in the refraction direction which can be computed using Snell's law), etc.

What's Next?

In the next chapter, we will learn how to initialize camera rays for each pixel of the frame, at which point all we need to do to get an image is to implement a simple ray-object intersection routine and store the result in an image file format.