Home

Interpolation

Distributed under the terms of the CC BY-NC-ND 4.0 License.

  1. Introduction
  2. Bilinear Filtering
  3. Trilinear Interpolation
  4. Source Code (external link GitHub)

Trilinear Interpolation

Reading time: 6 mins.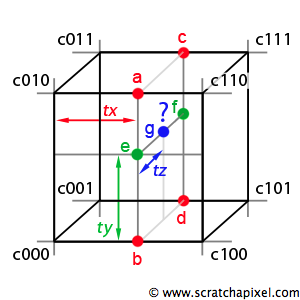
Figure 1: Trilinear interpolation. We perform four linear interpolations to compute a, b, c, and d using tx. Then we compute e and f by interpolating a, b, c, and d using ty, and finally, we find our sample point by interpolating e and f using tz.

Trilinear interpolation is a direct extension of the bilinear interpolation technique. It can be seen as the linear interpolation of two bilinear interpolations: one for the front face of the cell and one for the back face. To compute e and f, we use two bilinear interpolations with the techniques described in the previous chapter. To compute g, we linearly interpolate e and f along the z-axis (using tz, which is the z coordinate of the sample point g).

Trilinear interpolation has the same strengths and weaknesses as its 2D counterpart. It's fast and easy to implement, but it doesn't produce very smooth results. However, for volume rendering or fluid simulation, where a very large number of lookups in 3D grids are performed, it is still a very good choice.

Here is a simple example of trilinear interpolation on a grid. Note that, like with bilinear interpolation, the results can be computed as a series of operations (lines 43 to 45) or as a sum of the 8 corners of cells weighted by some coefficients (lines 47 to 55).

template<typename T> 
class Grid 
{ 
public: 
    unsigned nvoxels;  //number of voxels (cube) 
    unsigned nx, ny, nz;  //number of vertices 
    Vec3<T> *data; 
    Grid(unsigned nv = 10) : nvoxels(nv), data(NULL) 
    { 
        nx = ny = nz = nvoxels + 1; 
        data = new Vec3<t>[nx * ny * nz]; 
        for (int z = 0; z < nz + 1; ++z) { 
            for (int y = 0; y < ny + 1; ++y) { 
                for (int x = 0; x < nx + 1; ++x) { 
                    data[IX(x, y, z)] = Vec3<t>(drand48(), drand48(), drand48()); 
                } 
            } 
        } 
    } 
    ~Grid() { if (data) delete [] data; } 
    unsigned IX(unsigned x, unsigned y, unsigned z) 
    { 
        if (!(x < nx)) x -= 1; if (!(y < ny)) y -= 1; if (!(z < nz)) z -= 1; 
        return x * nx * ny + y * nx + z; 
    } 
    Vec3<T> interpolate(const Vec3<T>& location) 
    { 
        T gx, gy, gz, tx, ty, tz; 
        unsigned gxi, gyi, gzi; 
        // remap point coordinates to grid coordinates
        gx = location.x * nvoxels; gxi = int(gx); tx = gx - gxi; 
        gy = location.y * nvoxels; gyi = int(gy); ty = gy - gyi; 
        gz = location.z * nvoxels; gzi = int(gz); tz = gz - gzi; 
        const Vec3<T> & c000 = data[IX(gei, gyi, gzi)]; 
        const Vec3<T> & c100 = data[IX(gxi + 1, gyi, gzi)]; 
        const Vec3<T> & c010 = data[IX(gxi, gyi + 1, gzi)]; 
        const Vec3<T> & c110 = data[IX(gxi + 1, gyi + 1, gzi)]; 
        const Vec3<T> & c001 = data[IX(gxi, gyi, gzi + 1)]; 
        const Vec3<T> & c101 = data[IX(gxi + 1, gyi, gzi + 1)]; 
        const Vec3<T> & c011 = data[IX(gxi, gyi + 1, gzi + 1)]; 
        const Vec3<T> & c111 = data[IX(gxi + 1, gyi + 1, gzi + 1)]; 
#if 1 
        Vec3<T> e = bilinear<Vec3<T> >(tx, ty, c000, c100, c010, c110); 
        Vec3<T> f = bilinear<Vec3<T> >(tx, ty, c001, c101, c011, c111); 
        return e * ( 1 - tz) + f * tz; 
#else 
        return 
            (T(1) - tx) * (T(1) - ty) * (T(1) - tz) * c000 + 
            tx * (T(1) - ty) * (T(1) - tz) * c100 + 
            (T(1) - tx) * ty * (T(1) - tz) * c010 + 
            tx * ty * (T(1) - tz) * c110 + 
            (T(1) - tx) * (T(1) - ty) * tz * c001 + 
            tx * (T(1) - ty) * tz * c101 + 
            (T(1) - tx) * ty * tz * c011 + 
            tx * ty * tz * c111; 
#endif 
    } 
}; 
 
template<typename T> 
void testTrilinearInterpolation() 
{ 
    Grid<T> grid; 
    for (unsigned i = 0; i < 1000; ++i) { 
        // create a random location
        Vec3<T> result = grid.interpolate(Vec3<t>(drand48(), drand48(), drand48())); 
    } 
}

Implementation Details (2024 Update)

Since the lesson was first written, we have made some changes to the code (2024) to fix bugs. Checking the output of the code isn't as straightforward as it is with interpolation on 2D images. This is because 3D grids are mostly used to store and render volumetric objects, which requires a renderer that handles volumetrics to properly test the interpolation.

When the lesson was first written, the lesson on volume rendering wasn't available. This is no longer the case. We recommend checking the lesson on Volume Rendering to see a possible use case of 3D linear interpolation.

In the meantime, the code was improved to output a frame per slice in the output/upres grid. By looping through the output images, you can effectively see the result of the interpolation. Thanks to @kristopolous for this suggestion and making the changes to the code to support that idea.

Here is a visualization of the results that the program outputs. The initial 3D grid scr_grid3d has a resolution of 8x8x8, and the program aims to upres that grid to target_grid3d which is 128x128x128 in size. The program loops over every vertex of the upres grid (target_grid3d) and uses trilinear interpolation with data from the lower grid to set their own values. When you implement this technique, you need to be careful about a couple of things:

previous-