Introduction to Shading

Normals, Vertex Normals and Facing Ratio

Now that we reviewed the parameters that influence the appearance of objects (how bright they are, their color, etc.) we are ready to start studying some simple shading techniques.

Normals

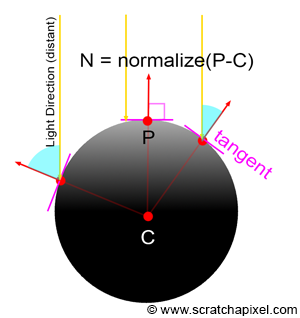
Normals play a central role in shading. Everybody knows that an object becomes brighter if we orient it towards a light source. The orientation of an object surface plays an important role in the amount of light it reflects (and thus how bright it looks like). This orientation can be represented at any point \(P\) on the surface of an object, by a normal \(N\) which is perpendicular to the surface at \(P\) as shown in figure 1\. Note in figure 1, how the brightness of the sphere decreases as the angle between the light direction and the normal increases. This decrease in brightness is something we can see everyday and yet probably few people know why it happens. We will explain the cause of this phenomenon in a short while. For now, you should only remember that:

• What we call normal (which we denote with the capital letter \(N\)) is the vector perpendicular to the surface tangent at \(P\) a point on the surface of the object. In other words, to find the normal at \(P\) we need to trace a line tangent to the surface at \(P\) and then take the vector perpendicular to that tangent line (note that in 3D, this would be tangent plane).

• That the brightness of a point on the surface of an object depends on the normal direction which defines the orientation of the object surface at that point with respect to the light. Another way of saying this, is that the brightness of the object at any given point of its surface depends on the angle between the normal at that point and the light direction.

The question now is how do we compute this normal? The complexity of the solution to this problem can be vary greatly depending on the type of geometry being rendered. The normal of the sphere can generally be easily found. If we know the position of the point on the surface of a sphere and the center of the sphere, the normal at this point can be computed by subtracting the point position from the sphere center:

Vec3f N = P - sphereCenter;

If the object is a triangle mesh, then each triangle defines a plane and the vector perpendicular to the plane is normal for any point lying on the surface of that triangle. The vector perpendicular to the triangle plane can easily be obtained with the cross product of two edges of that triangle. Keep in mind that v1xv2 = -v2xv1\. So the choice of edges will influence the direction of the normal. If you declare the triangle vertices in counterclockwise order, then you can use the following code:

Vec3f N = (v1-v0).crossProduct(v2-v0);

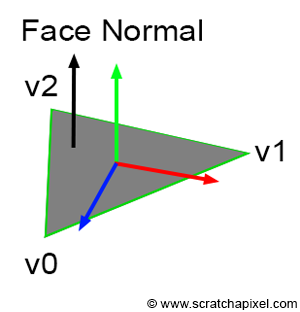
If the triangle lies in the xz plane, then the resulting normal should be (0,1,0) and not (0,-1,0) as shown in Figure 2

Computing the normal that way gives what we call a face normal (because the normal is the same for the entire face, regardless of the point you pick on that face or triangle). Normals of triangle meshes can also be defined at the vertices of the triangle, in which case we call these normals vertex normals. Vertex normals are used in a technique called smooth shading which you will find described at the end of this chapter. For now, we will only deal with face normals.

How and when in the program you compute the surface normal at the point you are about to shade doesn't matter. What matters and what is essential is that you have this information at hand when you are about to shade the point. In the few programs for this section in which we did some basic shading, we implemented a special method in every geometry class called getSurfaceProperties() in which we computed the normal at the intersection point (in case ray-tracing is used) and other variables such as the texture coordinates which we will talk about later in this lesson. Here is what the implementation of these methods could look like for the sphere and the triangle-mesh geometry type:

class Sphere : public Object 
{ 
    ... 
public: 
    ... 
    void getSurfaceProperties( 
        const Vec3f &hitPoint, 
        const Vec3f &viewDirection, 
        const uint32_t &triIndex, 
        const Vec2f &uv, 
        Vec3f &hitNormal, 
        Vec2f &hitTextureCoordinates) const 
    { 
        hitNormal= Phit - center; 
        hitNormal.normalize(); 
        ... 
    } 
    ... 
}; 
 
class TriangleMesh : public Object 
{ 
    ... 
public: 
    void getSurfaceProperties( 
        const Vec3f &hitPoint, 
        const Vec3f &viewDirection, 
        const uint32_t &triIndex, 
        const Vec2f &uv, 
        Vec3f &hitNormal, 
        Vec2f &hitTextureCoordinates) const 
    { 
        // face normal
        const Vec3f &v0 = P[trisIndex[triIndex * 3]]; 
        const Vec3f &v1 = P[trisIndex[triIndex * 3 + 1]]; 
        const Vec3f &v2 = P[trisIndex[triIndex * 3 + 2]]; 
        hitNormal = (v1 - v0).crossProduct(v2 - v0); 
        hitNormal.normalize(); 
        ... 
    } 
    ... 
}; 

A Simple Shading Effect: Facing Ratio

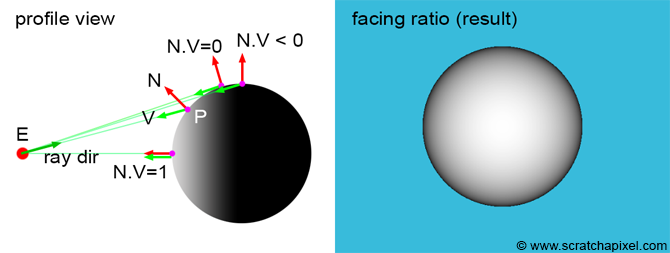
Now that we know how to compute the normal of a point on the surface of an object, we have enough information already to create a simple shading effect called facing ratio. This technique consists of computing the dot product of the normal of the point that we want to shade and the viewing direction. Computing the viewing direction is also very simple. When ray tracing is used, it is simply the opposite direction of the ray that intersected the surface at \(P\). If you don't use ray tracing, the viewing direction can also simply be found by tracing a line from the point on the surface \(P\) to the eye \(E\):

Vec3f V = (E - P).normalize(); // or -ray.dir if you use ray-tracing

Keep in mind that the dot product of two vectors returns 1 if the vectors are parallel and pointing in the same direction and 0 when the two vectors are perpendicular to each other. If the vectors point in opposite directions the dot product is negative, but if we use the result of this dot product as a color, then we are not interested in negative values anyway. If you need a reminder on the dot product, check the lesson on Geometry. To avoid negative results, we will need to clamp the result to 0:

float facingRatio = std::max(0, N.dotProduct(V));

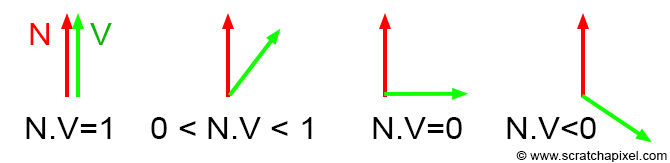
When the normal and the vector V point in the same direction then the dot product returns 1\. If the two vectors are perpendicular the result is 0\. If we use this simple technique to shade a sphere centered in the middle of the frame, then the center of the sphere will be white and the sphere will get darker as we move away from its center, towards the edge (as shown in the following figure).

Vec3f castRay( 
    const Vec3f &orig, const Vec3f &dir, 
    const std::vector<std::unique_ptr<Object>> &objects, 
    const Options &options) 
{ 
    Vec3f hitColor = options.backgroundColor; 
    float tnear = kInfinity; 
    Vec2f uv; 
    uint32_t index = 0; 
    Object *hitObject = nullptr; 
    if (trace(orig, dir, objects, tnear, index, uv, &hitObject)) { 
        Vec3f hitPoint = orig + dir * tnear;  //shaded point 
        Vec3f hitNormal; 
        Vec2f hitTexCoordinates; 
        // compute the normal of the point we want to shade
        hitObject->getSurfaceProperties(hitPoint, dir, index, uv, hitNormal, ...); 
        hitColor = std::max(0.f, hitNormal.dotProduct(-dir));  //facing ratio 
    } 
 
    return hitColor; 
} 

Congratulation! You have just learned about your first shading technique. Let's now learn about a more realistic shading method that will simulate the effect of light on a diffuse object. But before we learn about this method, we first need to introduce and learn about the concept of light.

Flat Shading vs. Smooth Shading and Vertex Normals

The problem with triangle meshes is that they can't represent perfectly smooth surfaces (unless the triangles are very small). If we wish to apply the facing-ratio technique we just described to a polygon mesh, we would need to compute the normal of the triangle intersected by the ray and compute the facing-ratio as the dot product between this face normal and the view direction. The problem with this approach is that it gives the object a faceted look as shown in the images below. This shading method is called for this reason flat shading

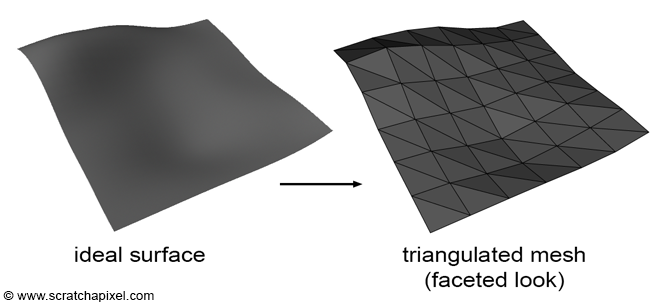
As mentioned a few times in the previous lessons, the normal of a triangle can simply be found, by computing the cross product of let's say the vector v0v1 and the vector v0v2, where v0, v1, and v2 represent the vertices of the triangle. To address this problem, Henri Gouraud introduced a method in 1971 which is now known as smooth shading, or Gouraud shading. The idea behind this technique is to produce continuous shading across the surface of a polygon mesh, even though precisely the object that the mesh represents is not continuous as it is built from a collection of flat surfaces (the polygons or the triangles). To do so, Gouraud introduced the concept of vertex normal. The idea is simple. Rather than computing or storing the normal for the face, we store a normal at each vertex of the mesh, where the orientation of the normal is determined by the underlying smooth surface that the triangle mesh was converted from. 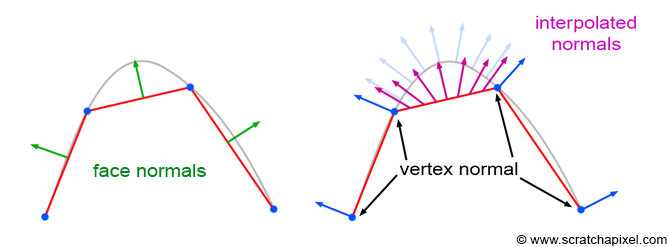When we want to compute the color of a point on the surface of a triangle, rather than using the face normal, we can compute a "fake smooth" normal by linearly interpolating the vertex normals defined at the triangle's vertices using the hit point barycentric coordinates.

The technique is illustrated in the image above. Vertex normals are defined at the vertices of the triangle. You can see that they are oriented perpendicular to the smooth underlying surface that the triangle mesh was built from. Sometimes triangles mesh are not directly converted from a smooth surface, and vertex normals have to be computed on the fly. Different techniques for computing vertex normals when there is no smooth surface to compute them from existence, but we won't study them in this lesson. For now, use software such as Maya or Blender to do this job for you (in Maya you can select your polygon mesh and select the option Soften Edge in the Normals menu).

In fact, from a practical and technical point of view, each triangle has its own set of 3 vertex normals. This means that the total of vertex normals for triangle mesh is equal to the number of triangles multiplied by 3. In some cases, the vertex normals defined on a vertex shared by 2, 3, or more triangles are the same (they point in the same direction) but you can achieve different effects by providing them different directions (you can for example fake some hard edges in the surface).

The source code for computing the interpolated normal on any point on the surface of a triangle is simple as long as we know the vertex normal for the triangle, the barycentric coordinates of this point on the triangle as well as the triangle index. Both the rasterization and the ray-tracing provide you with this information. Vertex normals are generated on the model by the 3D program that you have been using to create the model. They are then exported to the geometry file, with the triangle's connectivity information, the vertex positions, and the triangles' texture coordinates. All you need to do then is to combine the point barycentric coordinate and the triangle vertex normals to compute the point interpolated smooth normal (lines 17-20 below):

void getSurfaceProperties( 
    const Vec3f &hitPoint, 
    const Vec3f &viewDirection, 
    const uint32_t &triIndex, 
    const Vec2f &uv, 
    Vec3f &hitNormal, 
    Vec2f &hitTextureCoordinates) const 
{ 
    // face normal
    const Vec3f &v0 = P[trisIndex[triIndex * 3]]; 
    const Vec3f &v1 = P[trisIndex[triIndex * 3 + 1]]; 
    const Vec3f &v2 = P[trisIndex[triIndex * 3 + 2]]; 
    hitNormal = (v1 - v0).crossProduct(v2 - v0); 
 
#if 1 
    // compute "smooth" normal using Gouraud's technique (interpolate vertex normals)
    const Vec3f &n0 = N[trisIndex[triIndex * 3]]; 
    const Vec3f &n1 = N[trisIndex[triIndex * 3 + 1]]; 
    const Vec3f &n2 = N[trisIndex[triIndex * 3 + 2]]; 
    hitNormal = (1 - uv.x - uv.y) * n0 + uv.x * n1 + uv.y * n2; 
#endif 
 
    // doesn't need to be normalized as the N's are normalized but just for safety
    hitNormal.normalize(); 
 
    // texture coordinates
    const Vec2f &st0 = texCoordinates[trisIndex[triIndex * 3]]; 
    const Vec2f &st1 = texCoordinates[trisIndex[triIndex * 3 + 1]]; 
    const Vec2f &st2 = texCoordinates[trisIndex[triIndex * 3 + 2]]; 
    hitTextureCoordinates = (1 - uv.x - uv.y) * st0 + uv.x * st1 + uv.y * st2; 
} 

Note that this only produces the impression that the surface is smooth. If you look at the polygon sphere in the image below, you can still see that the silhouette is facetted, even though the surface appears smooth inside. The technique improves the look of triangle meshes but doesn't of course solve the problem of their faceted look completely. The only solution to this problem is to use a subdivision surface which we will talk about in a different section, or of course increase, the number of triangles used when smooth surfaces are converted to triangle meshes.

We are not ready to learn how to reproduce the appearance of diffuse surfaces. Though diffuse surfaces need light to be visible. Thus, before we can study this technique, we will first need to learn how we handle the concept of light sources in a 3D engine.