The Perspective and Orthographic Projection Matrix

Lost? Let's Recap With Real-World Production Examples

I realized after writing this chapter—more than 10 years after publishing the initial version of this lesson—that some of the concepts used in this chapter are not explained until the next chapter, notably concepts related to the GPU. While I could have moved this chapter after the following one, I decided to keep this order because it follows the chapter devoted to explaining how the perspective projection is built. Instead, I simply added this note to suggest that you read this chapter, then the next one, and eventually come back to this chapter after you have completed the next one. I know it may feel odd, but my experience with learning and teaching is that it has a lot to do with repetition and looking at the same problem from different points of view.

Why this chapter?

Recently (2024), I realized that some information regarding cameras was scattered across different lessons on the website. For example, the lesson on the pinhole camera discusses building a 3D camera from real-world data such as film width, height, and focal length. Meanwhile, the lesson on perspective projection also covers camera-related topics, but the connections between them weren't clearly established. There was no single place where these elements were effectively linked together, making it difficult to see how they all connect. This is the goal of this chapter, which was added years after the first version of the lesson.

The issue with building a perspective projection matrix that matches production tools such as Maya, Blender, or others is that they take into account a number of parameters. It's easy to forget how these parameters interact, and it's certainly easy to get confused. So, I decided to add this chapter later on, hoping to bridge the gap between these two lessons and clearly show how to build a perspective matrix according to those various parameters.

Namely, these input parameters can be:

• Whether you use a physical camera model to infer the camera's field or angle of view.

• Whether you use the field of view to calculate your screen coordinates.

• Whether you actually calculate the screen coordinates to build your perspective projection matrix or not.

• Whether you use a vertical or horizontal field of view.

• Finally, whether your film aspect ratio is different from your device (or screen) aspect ratio. This can be tricky if you want to mimic the various fit modes that some DCC tools, such as Maya, provide (e.g., fill, overscan, vertical, horizontal).

Again, this isn't rocket science, but I, like many other engineers, have lost countless hours trying to figure out why my results didn't match those of other tools. That's because the interplay of these parameters can be tricky to navigate when you're not Einstein or Wernher von Braun—since we were talking about rockets.

This chapter is also a great opportunity for you to review some of the concepts we learned earlier and, as I just mentioned, make connections with what you learned in the lesson on the Pinhole Camera Model.

There is also an interesting aspect of this work: as we go through the content, I will show you that, based on the results you obtain, you can deduce the meaning of some of the values displayed in tools like Maya or Blender. This will help you figure out the conventions they are effectively using. Nice!

Calculating the Field of View or Angle of View

If you start from a physical camera model, you will be provided with the film width and height. In the real world, these would be the size of your digital sensor, or if you still use celluloid film, the dimensions of your physical film. Let's take a basic format used in photography, which is the \(36 \text{mm} \times 24 \text{mm}\) format. The model should also provide you with the focal length. Let's use a focal length of \(38.601 \text{mm}\). These are the three required values. From there, and using simple trigonometry, we can calculate either the vertical or horizontal field of view:

The idea is to take, say, half of the width and divide it by the focal length. This is similar to calculating the tangent of the angle of a right triangle by taking the ratio of the triangle's opposite side to its adjacent side. All of this is explained in the lesson on the pinhole camera.

Okay, great—nothing really fancy here. You just need to be sure that your focal length and film dimensions are expressed in the same units. We use millimeters here. Let's do some math:

From which we find that:

I didn't choose these values randomly. I specifically wanted the horizontal field of view to be 50 degrees. Why? Because if you open a software like Maya and input the film width, height, and focal length values into the physical camera model, you will see that it calculates a parameter called the angle of view for you. With these numbers, the result will be 50 degrees, which allows you to infer that the angle of view displayed in the parameter list is the horizontal field of view, not the vertical one. That's important to know—believe me.

Great, so we have our angle of view. Note that not all tools provide you with the ability to use a physical camera model. Sometimes, all you have to control how much of the scene is visible is the angle of view. However, if you do have a physical camera model, you now know how to calculate the angle of view from it.

Also, keep in mind that the angle of view is not absolutely necessary for building a perspective projection matrix, as we will see later on. You can build the matrix using either set of parameters: the angle of view or the physical camera model parameters (film width, height, and focal length). The choice is yours. From the physical camera model parameters, you can calculate the angle of view, but from the angle of view alone, you cannot deduce the physical camera model parameters (such as calculating the width, the height or the focal length).

Now, let's move on to the screen coordinates.

Calculating the Screen Coordinates

The screen coordinates are the right, left, top, and bottom coordinates we've been using in the previous chapter to build our perspective projection matrix. Remember?

These are the boundaries of the view frustum in camera (view) space. They define the extent of the frustum at the near clipping plane. I will rename the terms \(\frac{2n}{r-l}\) and \(\frac{2n}{t-b}\) as \(\textcolor{red}{C}\) and \(\textcolor{red}{D}\), respectively."

These coordinates are easy to calculate because they are derived using the properties of similar triangles. Essentially, the ratio of the film width (divided by 2, since the screen coordinates are symmetrical) to the focal length is proportional to the right screen coordinate (assuming it's positive) to the near clipping plane distance.

From this, we can easily derive (Equation 1):

Similarly, we can calculate the top (the other positive) coordinate:

The left and bottom coordinates are just the negative counterparts of the right and top coordinates:

Simple! This method works if you start with the physical camera parameters—width, height, and focal length. But if you don't have those and only have the horizontal field of view (we'll focus on the horizontal case for now; we'll look into the vertical case next), then we need to use a different approach.

Given the angle of view, we know that:

Where \(\theta\) is half the angle of view. We can replace \(\frac{\text{film width} / 2}{\text{focal length}}\) in Equation 1 with \(\tan(\theta)\). We get:

Easy again. Now, the calculation of the top coordinate is a little more involved. Since we know the width of the screen (essentially \(\text{right} - \text{left}\)), we can calculate the total height by dividing this width by the image aspect ratio. Here, the image aspect ratio is the image width (in pixels) divided by the image height. Let's say our image is \(960 \times 540\) pixels (an aspect ratio of roughly \(1.777\)). Since the top coordinate is just half of the screen height, we need to divide that number by two.

Where \(\text{aspect}\) here is the image width (in pixels) divided by the image height (960/540). This is often referred to as the device aspect ratio.

Let's do some math (either method will give the same numbers, with \(Z_{\text{near}} = 0.1\)):

Great! So, what do we have now? Two methods to calculate the screen coordinates. Now, note something important: to calculate the field of view (angle of view), we started with the film dimensions (in mm) and the focal length (in mm). This film has its own aspect ratio, which in our example is \(36/24 = 1.5\). That aspect ratio is different from the aspect ratio of the image output resolution, which is 1.777. So, when you divide the screen width (\(\text{right} - \text{left}\)) by 1.777 (the device aspect ratio), what you're effectively doing is fitting the film gate within the resolution gate, as shown in the diagram below. This is an example of the fill fit mode.

I will now explain what's going on in terms of the pixel's journey through the pipeline, which is a good opportunity to review concepts such as the canvas, the near clipping plane, the frustum, clip space, homogeneous coordinates, etc. In short, we'll cover the whole shebang.

The Journey of a Vertex Down the Pipe

• Once upon a time, at the very origin of the computer graphics world, there was only a basic canvas with screen coordinates \(\{-1, -1, 1, 1\}\), respectively located 1 unit away from the eye or camera's origin. This is our very starting point. You can see that the screen is square, everything is 1 unit away, and to determine if a point is visible through that basic setup, all we need to do is divide its respective x and y coordinates by its z coordinate.

  Why does this work? Because if you divide the z-coordinate of the point by itself, you get 1. So effectively, the process of dividing the point's x and y coordinates by z projects the point onto a canvas that's 1 unit away from the eye. In other words, think of this as a near clipping plane set to 1. So, if a point is contained within the range \([-1, 1]\) in x and y after projection (after dividing the coordinates by the z-coordinate), then the point is visible on the canvas, as shown in the image below.

One important thing to note about this process is that the coordinates of the points visible on the screen all have their coordinates within the range \([-1, 1]\), as mentioned before. We can think of this as the points' coordinates being normalized, or, in other words, being within some kind of Normalized Device Coordinate (NDC) space. While this isn't exactly true, it helps in understanding what's coming next, so keep this in mind.

• Then came the idea of seeing more of the scene or being able to focus on one part of the scene in more detail without moving—what we call zooming out or in. One way to understand this process is in terms of scaling the canvas screen coordinates up or down, effectively enlarging or reducing the window through which we see the scene, as shown in the image below.

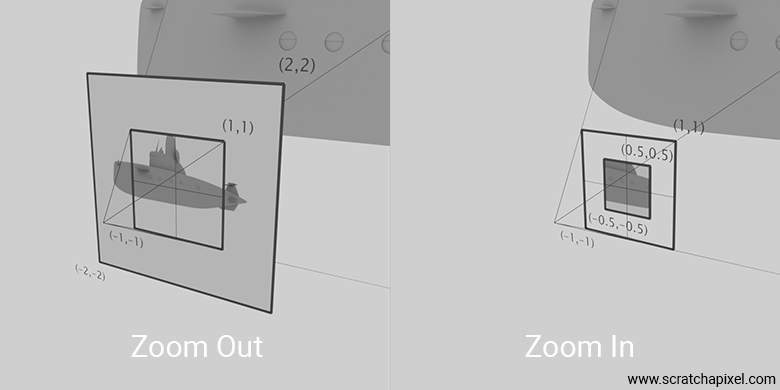
And how do we achieve this? By either taking a film that is smaller or larger—I mean the physical film here; think of it as a piece of paper that is sensitive to light. If you divide the film width by the focal length and that film width gets smaller, the right coordinate (and the absolute value of the left coordinate) will decrease, effectively producing a zoom-in effect. Similarly, if the width increases, the right/left coordinates increase, and so we achieve a zoom-out effect.

Or, by using the angle of view. Recall that \( \tan(\theta) = 1 \) when \( \theta = 45^\circ \). So, we have our \([-1, 1]\) screen coordinates when the angle of view is \(90^\circ\). For angles of view smaller than \(90^\circ\), the right/left (or absolute value of the left) coordinates decrease, resulting in a zoom-in effect. For angles greater than \(90^\circ\), the right/left coordinates increase, resulting in a zoom-out effect.

Good, good.

What I am aiming for here is for you to understand that how much of the scene you see depends only on the screen's right/left and top/bottom coordinates—nothing else. This is effectively controlled by the angle of view (or the film width). In this case, we use the horizontal angle of view, as mentioned earlier, or the film width. We will discuss using the film height or vertical field of view later.

Now you might ask, what's the point of the \(\textcolor{red}{C}\) and \(\textcolor{red}{D}\) coefficients in the perspective projection matrix then? Well, this is where the crux of the graphics pipeline lies. The goal of the GPU and the graphics pipeline is to determine what's visible on the screen and what's not. In other words, it needs to know what to clip and cull and what to preserve.

Okay, before we go any further, remember how we said earlier that when we projected our points onto our unit canvas (the canvas for which the screen coordinates are within the range \([-1,1]\)), it was somewhat like dealing with NDC (Normalized Device Coordinate) space. Now, note that if our screen coordinates are within the range \([-2,2]\) or \([-0.5,0.5]\), this has nothing to do with NDC space. Let's recall that points in NDC space have their coordinates normalized within the range \([-1,1]\).

So far, our vertex has gone from world space \(\rightarrow\) camera space. Then, we know how to project these onto the screen by dividing \(P.x\) and \(P.y\) by \(P.z\) respectively. We would keep the point if it's within the screen coordinates, but that's not what we're going to do. Instead, we'll make it so that only points whose x and y coordinates are in the range \([-1,1]\) are kept. The others will be discarded/cull. This process in the graphics pipeline corresponds to going from camera space \(\rightarrow\) NDC (Normalized Device Coordinate) space. How do we do that?

Well, this is where \(\textcolor{red}{C}\) and \(\textcolor{red}{D}\) come into play. Suppose our screen coordinates are \((-2,-2)\) and \((2,2)\) for the bottom-left and top-right corners, respectively. Recall that:

For now, we will assume that \(n\) (the near clipping plane) is equal to \(1\). So when we apply the perspective projection matrix to a vertex, the \(P.x\) and \(P.y\) coordinates of the point are effectively multiplied by \(\frac{1}{2}\) in this particular case. What does this mean? This means that after the perspective divide (once the point is divided by its z-coordinate), a point that was previously landing right on the top-right corner of the canvas—say, at screen coordinates \((2,2)\)—is now equal to \((1,1)\).

That's exactly what we want because now the point that is right on the edge (right at the corner, in this case) of the screen is effectively at the limit of the NDC range, which goes from \((-1,-1)\) to \((1,1)\). So, what \(\textcolor{red}{C}\) and \(\textcolor{red}{D}\) do is help remap the points being transformed to NDC space, which happens when we get to the perspective divide.

If you're still with me, congratulations!

Let's still ignore the near clipping plane for now. So, we now understand that the \(\textcolor{red}{C}\) and \(\textcolor{red}{D}\) terms in the perspective projection matrix are used to transform the vertex to NDC space. Though how this is done in the graphics pipeline of the GPU is a little more complex than it already seems.

There is something called clip space. When you apply the perspective projection matrix to a vertex, the vertex, right after this stage, lands in clip space. Welcome to clip space, vertex! Clip space is the space the vertex is in after projection but prior to the perspective divide. Now, this is where things get interesting. Recall that when you divide the vertex transformed by the perspective matrix by the point's (in camera space) z-coordinate, the point lands in NDC space (where we discard any point whose x and y coordinates are below -1 or above 1). So we have:

Recall that the perspective projection matrix has that little \(-1\) that I colored in green in the following equation:

Also, recall that when multiplying a point by a perspective matrix, we need to assume that the point has 4 coordinates, \(\{x, y, z, w\}\), where for Cartesian points, \(w = 1\). So we have:

If we expand, we get:

What I want you to see here is that the \(w\) coordinate of the transformed points holds the value of \(-z\). The reason for the minus sign is that in camera space, points that are in front of the camera all have their z-coordinates negative. So, negating it here turns the z-coordinate into a positive one. At this point in the pipeline, the vertex is said to be in clip space, and in that space, the vertex is expressed in terms of homogeneous coordinates. Let's recap: we go from world space → camera space → clip space. Then, we need to go from clip space → NDC space. We do so when we effectively convert the point from homogeneous coordinates back to a point with Cartesian coordinates, which involves normalizing its coordinates by \(w\), which, as you know, holds \(-z\). So this is effectively like a perspective divide:

Let's recap: world space → camera space → clip space → NDC space. Good. We are almost there. Note that when in NDC space, all points whose coordinates are below -1 or above 1 are not visible. So:

Since \(x\), \(y\), and \(z\) in NDC space were obtained by dividing the point's homogeneous coordinates by the \(w\) coordinate, we have:

And so we can write:

And that is exactly what the GPU does when the point is in clip space. This is why we speak of clipping. Any point whose coordinates for \(x\), \(y\), and \(z\) are lower than \(-w_{clip}\) or greater than \(w_{clip}\) are not visible and thus are culled (or clipped if we speak about a triangle whose vertices are out of the clipping volume). We say that \(w_{clip}\) defines the boundaries of the clipping volume, outside of which vertices are not visible, and inside of which vertices are visible. If two vertices connected to one another to form an edge straddle across that volume, then the edge gets clipped.

It's only after the vertex has passed that clipping stage, that the coordinates undergo the conversion from homogeneous coordinates to Cartesian coordinates, during which, as explained above, the perspective divide occurs—dividing the point's coordinate by the point's depth or z-coordinate.

If you're still here (and got it), then you can pat yourself on the back and treat yourself to something you've always wanted 🎉, because what we've just done is sum up 40 years of computer graphics development—at least when it comes to how GPUs have handled things from the 1980s up to today

• The final step in the process is the conversion of the vertex from NDC (Normalized Device Coordinates) space to Raster or Window space. The terminology—whether it's called Raster or Window space—can vary not only between different APIs but even within the same API over time, which can be confusing. However, it's generally referred to as one or the other. It's important to note that fragments in fragment shaders are defined in this space. Converting from NDC space to Raster space is straightforward: you multiply the NDC coordinates by one-half, add one-half, and then multiply that result by the image width (in pixels) for the x-coordinate and by the height for the y-coordinate. This gives you the position of the vertex in pixels, with decimal precision.

As you can see in the image above, images are rarely square; they are most often rectangular. So far, we have only considered canvases that were square. Now, let's explore what happens in the case of a rectangular canvas.

But Canvases Are Rarely Squared: C and D Again

By the way before we move forward, and because this will be useful for this particular topic and the following ones, let's do some more terminology definitiuoin work.

• Resolution Gate: this is the "gate" or "window" if you prefer, you can loo at it as a sheet of paper, as defined by the width and height of the image in terms of pixels. It's not so much the ndimension in pixels both in width and height that is relevant when we refer to the resolution gate, but mroe the aspect ration that these define. But when we speak about resolution gate, understand it as the "shape of the image" as defined by the width and heigh expressed in pixels. The image resolution.

• Film Gate: the is the counterpart to the resolution gate, but applied to the physical film or digital sensor of a camera. This is definied in physical units such as mm or inches. Again what we are interested in the most here is the ration between the film (cellilloid or sensor size for a digiral camera) width over its height. The film gate aspecr ratio.

With this defined, let's not see what's happening when the image isn't squared.

Now, remember that when the canvas is square, the screen coordinates for the top and right (and the absolute values of the bottom and left) are the same. If we assume the screen coordinates to be \((-1, -1)\) and \((1, 1)\) (which is possible for a film width/height of 20/20 and a focal length of 10, assuming a near clipping plane of 1), then note that both terms \(C\) and \(D\) will be 1:

So, \(C\) and \(D\) in this case do not affect the vertex \(P.x\) and \(P.y\) coordinates.

Remember, if the canvas is square, when remapped to NDC (Normalized Device Coordinates) space, the images formed by the vertices shouldn't be stretched. However, if the image resolution along the width is not the same as along the height, then when we go from NDC space \(\rightarrow\) raster space (which involves multiplying the normalized coordinates by the image width and height, respectively), our initially square image will become a rectangle, causing it to appear stretched (along the width if the image width is greater than the height), as shown in the image below.

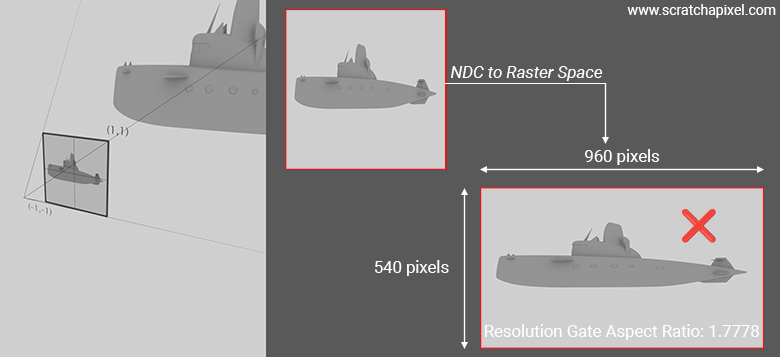
This is why the top/bottom and left/right screen coordinates need to reflect the resolution gate aspect ratio. Recall that:

With

So, when the screen coordinates are symmetrical, we can say that:

Then, we can calculate \(C\) and \(D\) as follows:

In other words, note that \(D\) will scale the vertices' y-coordinates by 1.7778, effectively creating an image that, if visible at this stage (though it isn't, since we only see the image after it's converted to raster/window space), is squeezed horizontally by the same ratio as the resolution gate aspect ratio. When we go from NDC space to raster space, the image undergoes a horizontal stretch (since the resolution width is greater than the resolution height, with a ratio of 1.7778). This stretch cancels out the initial squeeze (which was along the image width, resulting from scaling the vertices' y-coordinates by 1.7778), and the image as a result regains its correct proportions.

Quod Erat Demonstrandum.

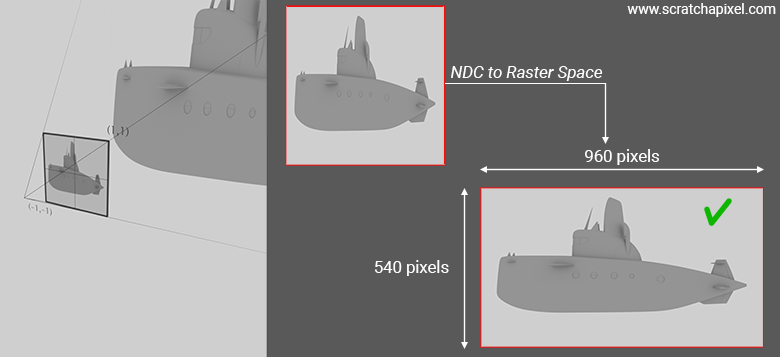
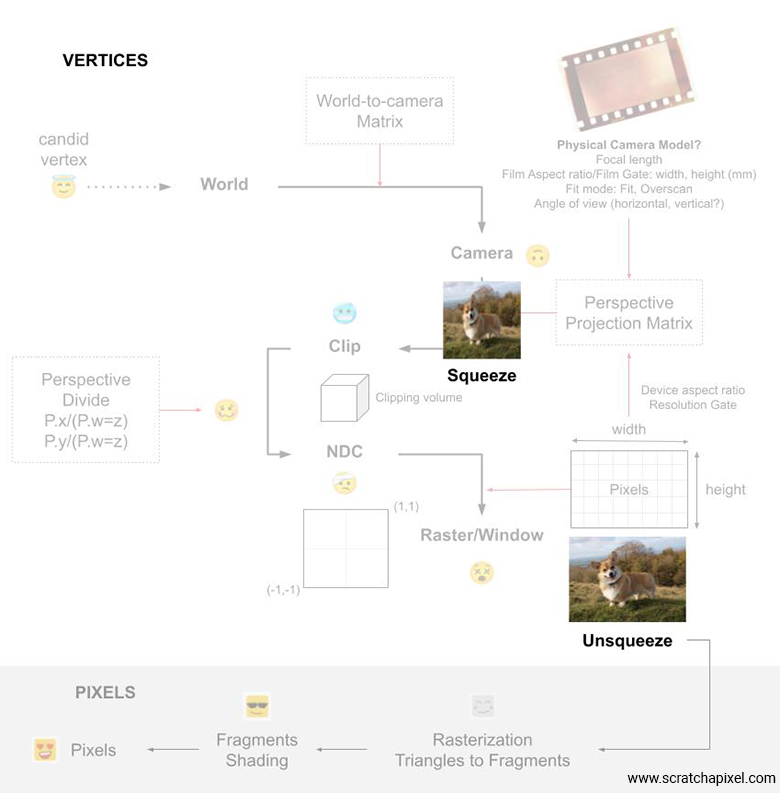
There’s something a bit confusing about what I just wrote, but I’ll keep it that way intentionally for the sake of the following explanation: don't be mistaken here; at this point in the pipeline, we're not yet dealing with pixels but still with vertices. When I say that the "image as a result regains its correct proportions," I mean that this will be true in the final image after the rendering process is complete. However, the conversion from NDC (Normalized Device Coordinates) to Raster space happens on vertices, not pixels. At this stage of the GPU pipeline, the rasterization process hasn't started yet. It’s only when the rasterization process begins, as shown in the image below, that triangles are converted into fragments, which ultimately become pixels. So, remember that all the transformations we've discussed so far are applied to vertices. In other words, we squeeze, scale, translate, and stretch vertices so they fit within various boxes or volumes of desired sizes and account for the final image or resolution gate aspect ratio. We can update our vertex pipeline diagram as follows:

The Near Clipping Plane

So far, for all our examples, we've chosen \( z_{\text{near}} = 1 \) mostly because it simplified our calculations for the screen coordinates. This meant that, in all cases, the canvas was virtually positioned 1 unit away from the eye. Of course, nothing stops us from moving this canvas anywhere along the line of sight, as shown in the figure below, which illustrates three different positions: one at \( z_{\text{near}} = 1 \), one where the distance to the eye is less than 1, and one where it's greater than 1. The resulting image is, of course, always the same; the only difference is that objects potentially located in front of the near clipping plane will be clipped or culled.

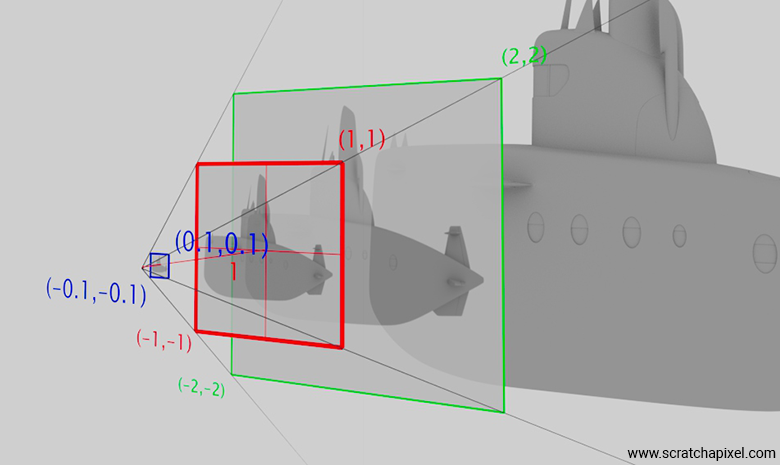
Now, all the \( z_{\text{near}} \) term does in the calculation of the screen coordinates (and later the \( C \) and \( D \) terms) is to scale the screen coordinates up or down according to its actual position with respect to the eye. This is simply another application of the similar triangles rule, where the ratio of the opposite sides of two similar triangles is equal to the ratio of their adjacent sides. When it comes to \( C \) and \( D \), the presence of \( n \) in the denominator accounts for the fact that we've used the \( z_{\text{near}} \) term for the screen coordinates in the numerator.

For example, say \( z_{\text{near}} \) is 0.1:

Then, when it comes to calculating \( C \) and \( D \):

We can generalize as follows:

As you can see, the \(2n\) in the numerator (top) of the equation to calculate \(C\) cancels out the \(2n\) in the denominator (bottom) that comes from calculating the right and left screen coordinates. The only factors that effectively affect both \(C\) and \(D\) are the angle of view and the resolution gate aspect ratio. Imagine, for example, that the angle of view is 80 degrees and the near clipping plane is 0.1. Then:

The Fit Mode

The last part we haven't covered yet regarding building a perspective projection matrix is something that is often not discussed at all. That's because it's mostly relevant for people using computer graphics in film production and doesn’t concern those solely interested in visualization or video games. This is the use of a feature that, in 3D DCC tools such as Maya, is called the fit mode.

This happens because the horizontal angle of view defines how much of the scene is visible, which is determined by the left and right screen coordinates. However, the top coordinate is determined by dividing the right coordinate by the image aspect ratio. The higher the ratio, the lower the top coordinate, and the less of the scene is visible vertically.

If the film gate and resolution gate aspect ratios are the same, both gates will show the same amount of the scene vertically. However, if the resolution aspect ratio is different from the film gate's, you will see less of the scene vertically through the resolution gate than through the film gate (assuming the resolution ratio is greater, as in our example with 1.7778 vs. 1.5). For example, if the right coordinate is 1, the top coordinate, using the resolution gate aspect ratio, becomes \( \frac{1}{1.7778} \approx 0.5624 \), which is less than the top coordinate when the film gate aspect ratio is used: \( \frac{1}{1.5} \approx 0.6667 \). Horizontally, the view remains the same, which is why this fit mode is referred to as the fill mode. Vertically, the image gets cropped.

Note that this is the result we get by default with the standard version of the function that builds the perspective projection matrix:

/* 
 * fw: film width in mm
 * fh: film height in mm
 * fl: focal length in mm
 * n: near clipping plane
 * f: far clipping plane
 * aspect: resolution aspect ratio (width in pixels / height in pixels)
 */
void mat4x4_perspective(mat4x4 m, float fw, float fh, float fl, float n, float f, float aspect) {
    // fill fit mode
    float r = (fw * 0.5) / fl * n;
    float l = -r;
    float t = ((r - l) / aspect) / 2;
    float b = -t;

    m[0][0] = 2 * n / (r - l);
    m[0][1] = 0;
    m[0][2] = 0;
    m[0][3] = 0;
    
    m[1][0] = 0;
    m[1][1] = 2 * n / (t - b);
    m[1][2] = 0;
    m[1][3] = 0;
    
    m[2][0] = 0;
    m[2][1] = 0;
    m[2][2] = -((f + n) / (f - n));
    m[2][3] = -1.f;
    
    m[3][0] = 0;
    m[3][1] = 0;
    m[3][2] = -((2.f * f * n) / (f - n));
    m[3][3] = 0;
}

In some cases, you might prefer the resolution gate to fit the film gate vertically. This is possible but requires adjusting the left and right coordinates of the resolution gate while keeping the top and bottom screen coordinates of the film gate. Note that this is only feasible if you have information about both the resolution aspect ratio (which we typically have since we always know the output image resolution) and the film gate aspect ratio. If you don't have the latter, you won't be able to implement this other mode, which, in contrast to the fill mode, is called the overscan mode. As you can see in the following image, which shows the same scene rendered with the overscan mode, we can see more of the scene to the left and right while seeing the same amount of the scene vertically. To implement this mode, at a minimum, you need to know the film gate aspect ratio in addition to the resolution gate ratio, and multiply the left/right coordinates calculated from the horizontal angle of view by the ratio \(1.7778 / 1.5\) in our example.

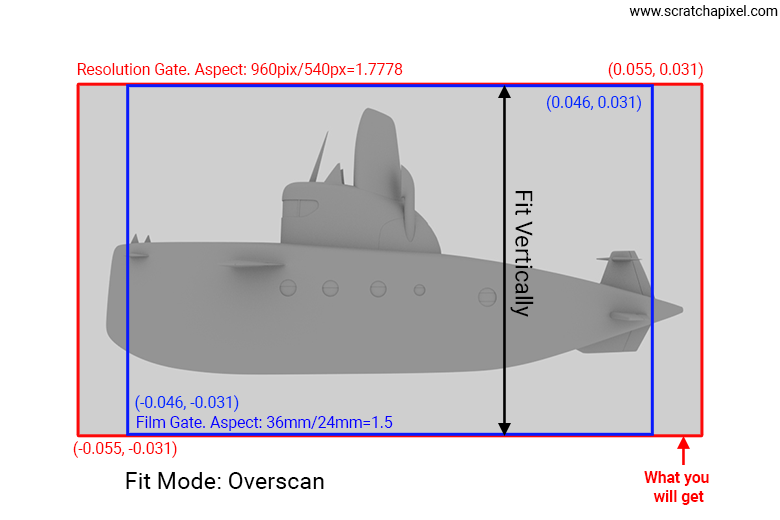
Of course, to implement this fully, you will need to account for whether the film gate ratio is greater or lower than the resolution gate aspect ratio, but we'll leave this as an exercise for you to do.

/* 
 * fw: film width in mm
 * fh: film height in mm
 * fl: focal length in mm
 * n: near clipping plane
 * f: far clipping plane
 * aspect: resolution aspect ratio (width in pixels / height in pixels)
 */
void mat4x4_perspective(mat4x4 m, float fw, float fh, float fl, float n, float f, float resolution_aspect_ratio) {
    // overscan fit mode
    float film_aspect_ratio = fw / fh; /* fw > fh */
    float xscale = resolution_aspect_ratio / film_aspect_ratio; /* resolution_aspect_ratio > film_aspect_ratio */
    float r = (fw * 0.5) / fl * n * xscale;
    float l = -r;
    float t = ((r - l) / resolution_aspect_ratio) / 2;
    float b = -t;

    m[0][0] = 2 * n / (r - l);
    m[0][1] = 0;
    m[0][2] = 0;
    m[0][3] = 0;
    
    m[1][0] = 0;
    m[1][1] = 2 * n / (t - b);
    m[1][2] = 0;
    m[1][3] = 0;
    
    m[2][0] = 0;
    m[2][1] = 0;
    m[2][2] = -((f + n) / (f - n));
    m[2][3] = -1.f;
    
    m[3][0] = 0;
    m[3][1] = 0;
    m[3][2] = -((2.f * f * n) / (f - n));
    m[3][3] = 0;
}

This hopefully covers everything we want to consider regarding the various parameters and settings (such as the fit mode) that can affect the perspective projection matrix. There are two last topics we will look into before we wrap up: what to do if we prefer to work with a vertical field of view, which some APIs like OpenGL tend to use by convention, and some faster ways by which the screen coordinates and coefficients \(C\) and \(D\) of the perspective matrix can be calculated.

Takeaways

That's about hundreds of pages of material on perspective projection matrices summarized in 20 lines. And that's ALL you need to remember about the perspective projection matrix.

Vertical vs Horizontal Field of View

As is usual with computer graphics, most systems use their own set of conventions that differ from others. Whether the angle of view refers to the horizontal or vertical angle of view is no exception. Maya, for instance, refers to the angle of view as the horizontal one, whereas the OpenGL specifications expect the angle of view to be vertical. There's nothing we can do about it. All I have done to help you is underline that if you have access to the physical film width and height, and the focal length, and if your tool additionally displays a value for the angle of view, you can calculate the angle of view yourself from the physical film properties and then compare your values against those of the tool. You will then be able to make a good guess as to whether your tool uses a vertical or horizontal angle of view.

If you use a vertical angle of view, then the top and bottom screen coordinates will be calculated from that angle. We can simply obtain the right coordinate by multiplying the top coordinate by the resolution gate aspect ratio. Similarly, if you do a bit of math, you will find that:

Optimizations

The motivation behind writing this chapter was this code (I know, so many words for just a few lines of code):

LINMATH_H_FUNC void mat4x4_perspective(mat4x4 m, float y_fov, float aspect, float n, float f)
{
	/* NOTE: Degrees are an unhandy unit to work with.
	 * linmath.h uses radians for everything! */
	float const a = 1.f / tanf(y_fov / 2.f);

	m[0][0] = a / aspect;
	m[0][1] = 0.f;
	m[0][2] = 0.f;
	m[0][3] = 0.f;

	m[1][0] = 0.f;
	m[1][1] = a;
	m[1][2] = 0.f;
	m[1][3] = 0.f;

	m[2][0] = 0.f;
	m[2][1] = 0.f;
	m[2][2] = -((f + n) / (f - n));
	m[2][3] = -1.f;

	m[3][0] = 0.f;
	m[3][1] = 0.f;
	m[3][2] = -((2.f * f * n) / (f - n));
	m[3][3] = 0.f;
}

An intern I was working with couldn't wrap his head around it. While I generally try to redirect them to an existing page on Scratchapixel, I found that there was no page on the website that clearly explained the role of each non-zero coefficient in the perspective projection matrix, or, as explained in the preamble, the relationship between the various parameters that make up a camera model, particularly a physical one, and that matrix. So, I decided to add this chapter to fill that gap. Hopefully, it will successfully clear up many of the puzzling questions you may have had regarding this mysterious matrix and how it fits into the GPU vertex pipeline. However, there's one last thing—the use of the tan function—which we need to explain. It’s simply shorthand for:

Where \(x_{\text{fov}}\) and \(y_{\text{fov}}\) stand for the horizontal and vertical field of view, respectively. Half of the film width divided by the focal length is simply an application of basic trigonometry, where the tangent of a right triangle's angle is equal to the ratio of the opposite side to its adjacent side (the focal length). Now, when we calculate \(C\), we get:

Of course, the code above uses a vertical angle of view, whereas the equation assumes a horizontal angle of view.

Wrapping Up

Next time you come across code like this:

template <class T>
inline void
Frustum<T>::set (T nearPlane, T farPlane, T fovx, T fovy, T aspect)
    IMATH_NOEXCEPT
{
    const T two = static_cast<T> (2);

    if (fovx != T (0))
    {
        _right  = nearPlane * std::tan (fovx / two);
        _left   = -_right;
        _top    = ((_right - _left) / aspect) / two;
        _bottom = -_top;
    }
    else
    {
        _top    = nearPlane * std::tan (fovy / two);
        _bottom = -_top;
        _right  = (_top - _bottom) * aspect / two;
        _left   = -_right;
    }
    _nearPlane    = nearPlane;
    _farPlane     = farPlane;
    _orthographic = false;
}

or

template <class T>
IMATH_CONSTEXPR14 inline Matrix44<T>
Frustum<T>::projectionMatrix () const IMATH_NOEXCEPT
{
    T rightPlusLeft  = _right + _left;
    T rightMinusLeft = _right - _left;

    T topPlusBottom  = _top + _bottom;
    T topMinusBottom = _top - _bottom;

    T farPlusNear  = _farPlane + _nearPlane;
    T farMinusNear = _farPlane - _nearPlane;

    if (_orthographic)
    {
        T tx = -rightPlusLeft / rightMinusLeft;
        T ty = -topPlusBottom / topMinusBottom;
        T tz = -farPlusNear / farMinusNear;

        T A = T (2) / rightMinusLeft;
        T B = T (2) / topMinusBottom;
        T C = T (-2) / farMinusNear;

        return Matrix44<T> (
            A, 0, 0, 0, 0, B, 0, 0, 0, 0, C, 0, tx, ty, tz, 1.f);
    }
    else
    {
        T A = rightPlusLeft / rightMinusLeft;
        T B = topPlusBottom / topMinusBottom;
        T C = -farPlusNear / farMinusNear;

        T farTimesNear = T (-2) * _farPlane * _nearPlane;

        T D = farTimesNear / farMinusNear;

        T twoTimesNear = T (2) * _nearPlane;

        T E = twoTimesNear / rightMinusLeft;
        T F = twoTimesNear / topMinusBottom;

        return Matrix44<T> (E, 0, 0, 0, 0, F, 0, 0, A, B, C, -1, 0, 0, D, 0);
    }
}

which comes from the Imath library, a library initially developed by ILM (Industrial Light & Magic) and quite popular among the community of developers writing 3D software for film and VFX, the code will hold no secrets for you.