Rasterization: a Practical Implementation

An Overview of the Rasterization Algorithm

Everything You Wanted to Know About the Rasterization Algorithm (But Were Afraid to Ask!)

The rasterization rendering technique is surely the most commonly used technique to render images of 3D scenes, and yet, that is probably the least understood and the least properly documented technique of all (especially compared to ray-tracing).

Why this is so, depends on different factors. First, it's a technique from the past. We don't mean to say the technique is obsolete, quite the contrary, but that most of the techniques that are used to produce an image with this algorithm, were developed somewhere between the 1960s and the early 1980s. In the world of computer graphics, this is middle-ages and the knowledge about the papers in which these techniques were developed tends to be lost. Rasterization is also the technique used by GPUs to produce 3D graphics. Hardware technology changed a lot since GPUs were first invented, but the fondamental techniques they implement to produce images haven't changed much since the early 1980s (the hardware changed, but the underlying pipeline by which an image is formed hasn't). In fact, these techniques are so fundamental and consequently so deeply integrated within the hardware architecture, that no one pays attention to them anymore (only people designing GPUs can tell what they do, and this is far from being a trivial task, but designing a GPU and understanding the principle of the rasterization algorithm are two different things; thus explaining the latter should not be that hard!).

Regardless, we thought it was urgent and important to correct this situation. With this lesson, we believe it to be the first resource that provides a clear and complete picture of the algorithm as well as a full practical implementation of the technique. If you found in this lesson the answers you have been desperately looking for anywhere else, please consider donating! This work is provided to you for free and requires many hours of hard work.

Introduction

Rasterization and ray tracing try to solve the visibility or hidden surface problem but in a different order (the visibility problem was introduced in the lesson Rendering an Image of a 3D Scene, an Overview). Both algorithms have in common that they essentially use techniques from geometry to solve that problem. In this lesson, we will describe briefly how the rasterization (you can write rasterization if you prefer UK English to US English) algorithm works. Understanding the principle is quite simple but implementing it requires to use of a series of techniques notably from the field of geometry, that you will also find explained in this lesson.

The program we will develop in this lesson to demonstrate how rasterization works in practice is important, because we will use it again in the next lessons to implement the ray-tracing algorithm as well. Having both algorithms implemented in the same program will allow us to more easily compare the output produced by the two rendering techniques (they should both produce the same result at least before shading is applied) and performances. It will be a great way to better understand the pros and cons of both algorithms.

The Rasterization Algorithm

There are not one but multiple rasterization algorithms, but to go straight to the point, let's say that all these different algorithms though are based upon the same overall principle. In other words, all these algorithms are just variants of the same idea. It is this idea or principle, we will refer to when we speak of rasterization in this lesson.

What is that idea? In the previous lessons, we already talked about the difference between rasterization and ray-tracing. We also suggested that the rendering process can essentially be decomposed into two main tasks: visibility and shading. Rasterization to say things quickly is essentially a method to solve the visibility problem. Visibility consists of being able to tell which parts of 3D objects are visible to the camera. Some parts of these objects can be bidden because they are either outside the camera's visible area or hidden by other objects.

Solving this problem can be done in essentially two ways. You can either trace a ray through every pixel in the image to find out the distance between the camera and any object this ray intersects (if any). The object visible through that pixel is the object with the smallest intersection distance (generally denoted t). This is the technique used in ray tracing. Note that in this particular case, you create an image by looping over all pixels in the image, tracing a ray for each one of these pixels, and then finding out if these rays intersect any of the objects in the scene. In other words, the algorithm requires two main loops. The outer loop iterates over the pixel in the image, and the inner loop iterates over the objects in the scene:

for (each pixel in the image) { 
    Ray R = computeRayPassingThroughPixel(x,y); 
    float tclosest = INFINITY; 
    Triangle triangleClosest = NULL; 
    for (each triangle in the scene) { 
        float thit; 
        if (intersect(R, object, thit)) { 
             if (thit < closest) { 
                 triangleClosest = triangle; 
             } 
        } 
    } 
    if (triangleClosest) { 
        imageAtPixel(x,y) = triangleColorAtHitPoint(triangle, tclosest); 
    } 
} 

Note that in this example, the objects are considered to be made of triangles (and triangles only). Rather than iterating other objects, we just consider the objects as a pool of triangles and iterate other triangles instead. For reasons we have already explained in the previous lessons, the triangle is often used as the basic rendering primitive both in ray tracing and in rasterization (GPUs require the geometry to be triangulated).

Ray tracing is the first possible approach to solve the visibility problem. We say the technique is image-centric because we shoot rays from the camera into the scene (we start from the image) as opposed to the other way around, which is the approach we will be using in rasterization.

Rasterization takes the opposite approach. To solve for visibility, it actually "projects" triangles onto the screen, in other words, we go from a 3D representation to a 2D representation of that triangle, using perspective projection. This can easily be done by projecting the vertices making up the triangle onto the screen (using perspective projection as we just explained). The next step in the algorithm is to use some technique to fill up all the pixels of the image that are covered by that 2D triangle. These two steps are illustrated in Figure 2. From a technical point of view, they are very simple to perform. The projection steps only require a perspective divide and a remapping of the resulting coordinates from image space to raster space, a process we already covered in the previous lessons. Finding out which pixels in the image the resulting triangles cover, is also very simple and will be described later.

What does the algorithm look like compared to the ray tracing approach? First, note that rather than iterating over all the pixels in the image first, in rasterization, in the outer loop, we need to iterate over all the triangles in the scene. Then, in the inner loop, we iterate over all pixels in the image and find out if the current pixel is "contained" within the "projected image" of the current triangle (figure 2). In other words, the inner and outer loops of the two algorithms are swapped.

// rasterization algorithm
for (each triangle in scene) { 
    // STEP 1: project vertices of the triangle using perspective projection
    Vec2f v0 = perspectiveProject(triangle[i].v0); 
    Vec2f v1 = perspectiveProject(triangle[i].v1); 
    Vec2f v2 = perspectiveProject(triangle[i].v2); 
    for (each pixel in image) { 
        // STEP 2: is this pixel contained in the projected image of the triangle?
        if (pixelContainedIn2DTriangle(v0, v1, v2, x, y)) { 
            image(x,y) = triangle[i].color; 
        } 
    } 
}

This algorithm is object-centric because we actually start from the geometry and walk our way back to the image as opposed to the approach used in ray tracing where we started from the image and walked our way back into the scene.

Both algorithms are simple in their principle, but they differ slightly in their complexity when it comes to implementing them and finding solutions to the different problems they require to solve. In ray tracing, generating the rays is simple but finding the intersection of the ray with the geometry can reveal itself to be difficult (depending on the type of geometry you deal with) and is also potentially computationally expensive. But let's ignore ray tracing for now. In the rasterization algorithm, we need to project vertices onto the screen which is simple and fast, and we will see that the second step which requires finding out if a pixel is contained within the 2D representation of a triangle has an equally simple geometric solution. In other words, computing an image using the rasterization approach relies on two very simple and fast techniques (the perspective process and finding out if a pixel lies within a 2D triangle). Rasterization is a good example of an "elegant" algorithm. The techniques it relies on have simple solutions; they are also easy to implement and produce predictable results. For all these reasons, the algorithm is very well suited for the GPU and is the rendering technique applied by GPUs to generate images of 3D objects (it can also easily be run in parallel).

In summary:

• Converting geometry to triangles makes the process simpler. If all primitives are converted to the triangle primitive, we can write fast and efficient functions to project triangles onto the screen and check if pixels lie within these 2D triangles

• Rasterization is object-centric. We project geometry onto the screen and determine their visibility by looping over all pixels in the image.

• It relies on mostly two techniques: projecting vertices onto the screen and finding out if a given pixel lies within a 2D triangle.

• The rendering pipeline run on GPUs is based on the rasterization algorithm.

The fast rendering of 3D Z-buffered linearly interpolated polygons is a problem that is fundamental to state-of-the-art workstations. In general, the problem consists of two parts: 1) the 3D transformation, projection, and light calculation of the vertices, and 2) the rasterization of the polygon into a frame buffer. (A Parallel Algorithm for Polygon Rasterization, Juan Pineda - 1988)

The term rasterization comes from the fact that polygons (triangles in this case) are decomposed in a way, into pixels, and as we know an image made of pixels is called a raster image. Technically this process is referred to as the rasterization of the triangles into an image of frame buffer.

Rasterization is the process of determining which pixels are inside a triangle, and nothing more. (Michael Abrash in Rasterization on Larrabee)

Hopefully, at this point of the lesson, you have understood the way the image of a 3D scene (made of triangles) is generated using the rasterization approach. Of course, what we described so far is the simplest form of the algorithm. First, it can be optimized greatly but furthermore, we haven't explained yet what happens when two triangles projected onto the screen overlap the same pixels in the image. When that happens, how do we define which one of these two (or more) triangles is visible to the camera? We will now answer these two questions.

Optimizing: 2D Triangles Bounding Box

The problem with the naive implementation of the rasterization algorithm we gave so far, is that it requires in the inner loop to iterate over all pixels in the image, even though only a small number of these pixels may be contained within the triangle (as shown in figure 3). Of course, this depends on the size of the triangle on the screen. But considering we are not interested in rendering one triangle but an object made up of potentially from a few hundred to a few million triangles, it is unlikely that in a typical production example, these triangles will be very large in the image.

There are different ways of minimizing the number of tested pixels, but the most common one consists of computing the 2D bounding box of the projected triangle and iterating over the pixels contained in that 2D bounding box rather than the pixels of the entire image. While some of these pixels might still lie outside the triangle, at least on average, it can already considerably improve the performance of the algorithm. This idea is illustrated in figure 3.

Computing the 2D bounding box of a triangle is very simple. We just need to find the minimum and maximum x- and y-coordinates of the three vertices making up the triangle in raster space. This is illustrated in the following pseudo code:

// convert the vertices of the current triangle to raster space
Vec2f bbmin = INFINITY, bbmax = -INFINITY; 
Vec2f vproj[3]; 
for (int i = 0; i < 3; ++i) { 
    vproj[i] = projectAndConvertToNDC(triangle[i].v[i]); 
    // coordinates are in raster space but still floats not integers
    vproj[i].x *= imageWidth; 
    vproj[i].y *= imageHeight; 
    if (vproj[i].x < bbmin.x) bbmin.x = vproj[i].x); 
    if (vproj[i].y < bbmin.y) bbmin.y = vproj[i].y); 
    if (vproj[i].x > bbmax.x) bbmax.x = vproj[i].x); 
    if (vproj[i].y > bbmax.y) bbmax.y = vproj[i].y); 
} 

Once we calculated the 2D bounding box of the triangle (in raster space), we just need to loop over the pixel defined by that box. But you need to be very careful about the way you convert the raster coordinates, which in our code are defined as floats rather than integers. First, note that one or two vertices may be projected outside the boundaries of the canvas. Thus, their raster coordinates may be lower than 0 or greater than the image size. We solve this problem by clamping the pixel coordinates to the range [0, Image Width - 1] for the x coordinate, and [0, Image Height - 1] for the y coordinate. Furthermore, we will need to round off the minimum and maximum coordinates of the bounding box to the nearest integer value (note that this works fine when we iterate over the pixels in the loop because we initialize the variable to xmim or ymin and break from the loop when the variable x or y is lower or equal to xmax or ymax). All these tests need to be applied before using the final fixed point (or integer) bounding box coordinates in the loop. Here is the pseudo-code:

... 
uint xmin = std::max(0, std:min(imageWidth - 1, std::floor(min.x))); 
uint ymin = std::max(0, std:min(imageHeight - 1, std::floor(min.y))); 
uint xmax = std::max(0, std:min(imageWidth - 1, std::floor(max.x))); 
uint ymax = std::max(0, std:min(imageHeight - 1, std::floor(max.y))); 
for (y = ymin; y <= ymin; ++y) { 
    for (x = xmin; x <= xmax; ++x) { 
        // check of if current pixel lies in triangle
        if (pixelContainedIn2DTriangle(v0, v1, v2, x, y)) { 
            image(x,y) = triangle[i].color; 
        } 
    } 
} 

The Image or Frame-Buffer

Our goal is to produce an image of the scene. We have two ways of visualizing the result of the program, either by displaying the rendered image directly on the screen or saving the image to disk, and using a program such as Photoshop to preview the image later on. But in both cases though, we somehow need to store the image that is being rendered while it's being rendered and for that purpose, we use what we call in CG an image or frame-buffer. It is nothing else than a two-dimensional array of colors that has the size of the image. Before the rendering process starts, the frame-buffer is created and the pixels are all set to black. At render time, when the triangles are rasterized, if a given pixel overlaps a given triangle, then we store the color of that triangle in the frame-buffer at that pixel location. When all triangles have been rasterized, the frame-buffer will contain the image of the scene. All that is left to do then is either display the content of the buffer on the screen or save its content to a file. In this lesson, we will choose the latter option.

When Two Triangles Overlap the Same Pixel: The Depth Buffer (or Z-Buffer)

Keep in mind that the goal of the rasterization algorithm is to solve the visibility problem. To display 3D objects, it is necessary to determine which surfaces are visible. In the early days of computer graphics, two methods were used to solve the "hidden surface" problem (the other name for the visibility problem): the Newell algorithm and the z-buffer. We only mention the Newell algorithm for historical reasons but we won't study it in this lesson because it is not used anymore. We will only study the z-buffer method which is used by GPUs.

There is one last thing though that we need to do to get a basic rasterizer working. We need to account for the fact that more than one triangle may overlap the same pixel in the image (as shown in figure 5). When this happens, how do we decide which triangle is visible? The solution to this problem is very simple. We will use what we call a z-buffer which is also called a depth buffer, two terms that you may have heard or read about already quite often. A z-buffer is nothing more than another two-dimensional array that has the same dimension as the image, however rather than being an array of colors, it is simply an array of floating numbers. Before we start rendering the image, we initialize each pixel in this array to a very large number. When a pixel overlaps a triangle, we also read the value stored in the z-buffer at that pixel location. As you maybe guessed, this array is used to store the distance from the camera to the nearest triangle that any pixel in the image overlaps. Since this value is initially set to infinity (or any very large number), then, of course, the first time we find that a given pixel X overlaps a triangle T1, the distance from the camera to that triangle is necessarily lower than the value stored in the z-buffer. What we do then, is replace the value stored for that pixel with the distance to T1. Next, when the same pixel X is tested and we find that it overlaps another triangle T2, we then compare the distance of the camera to this new triangle to the distance stored in the z-buffer (which at this point, stores to the distance to the first triangle T1). If this distance to the second triangle is lower than the distance to the first triangle, then T2 is visible and T1 is hidden by T2. Otherwise, T1 is hidden by T2, and T2 is visible. In the first case, we update the value in the z-buffer with the distance to T2 and in the second case, the z-buffer doesn't need to be updated since the first triangle T1 is still the closest triangle we found for that pixel so far. As you can see the z-buffer is used to store the distance of each pixel to the nearest object in the scene (we don't really use the distance, but we will give the details further in the lesson). In figure 5, we can see that the red triangle is behind the green triangle in 3D space. If we were to render the red triangle first, and the green triangle second, for a pixel that would overlap both triangles, we would have to store in the z-buffer at that pixel location, first a very large number (that happens when the z-buffer is initialized), then the distance to the red triangle and then finally the distance to the green triangle.

You may wonder how we find the distance from the camera to the triangle. Let's first look at an implementation of this algorithm in pseudo-code and we will come back to this point later (for now let's just assume the function pixelContainedIn2DTriangle computes that distance for us):

// A z-buffer is just an 2D array of floats
float buffer = new float [imageWidth * imageHeight]; 
// initialize the distance for each pixel to a very large number
for (uint32_t i = 0; i < imageWidth * imageHeight; ++i) 
    buffer[i] = INFINITY; 
 
for (each triangle in scene) { 
    // project vertices
    ... 
    // compute bbox of the projected triangle
    ... 
    for (y = ymin; y <= ymin; ++y) { 
        for (x = xmin; x <= xmax; ++x) { 
            // check of if current pixel lies in triangle
            float z;  //distance from the camera to the triangle 
            if (pixelContainedIn2DTriangle(v0, v1, v2, x, y, z)) { 
                // If the distance to that triangle is lower than the distance stored in the
                // z-buffer, update the z-buffer and update the image at pixel location (x,y)
                // with the color of that triangle
                if (z < zbuffer(x,y)) { 
                    zbuffer(x,y) = z; 
                    image(x,y) = triangle[i].color; 
                } 
            } 
        } 
    } 
} 

What's Next?

This is only a very high-level description of the algorithm (figure 6) but this should hopefully already give you an idea of what we will need in the program to produce an image. We will need:

• An image-buffer (a 2D array of colors),

• A depth-buffer (a 2D array of floats),

• Triangles (the geometry making up the scene),

• A function to project vertices of the triangles onto the canvas,

• A function to rasterize the projected triangles,

• Some code to save the content of the image buffer to disk.

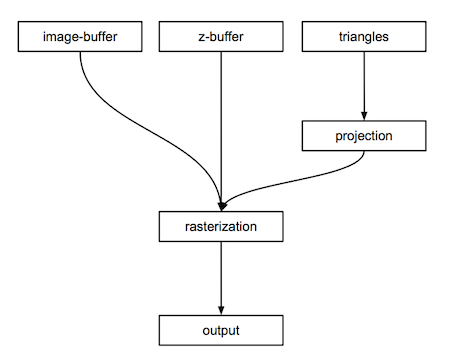
In the next chapter, we will see how are coordinates converted from camera to raster space. The method is of course identical to the one we studied and presented in the previous lesson, however, we will present a few more tricks along the way. In chapter three, we will learn how to rasterize triangles. In chapter four, we will study in detail how the z-buffer algorithm works. As usual, we will conclude this lesson with a practical example.