Implementing the Raytracing Algorithm
Reading time: 5 mins.Armed with an understanding of light-matter interactions, cameras and digital images, we are poised to construct our very first ray tracer. This chapter will delve into the heart of the ray-tracing algorithm, laying the groundwork for our exploration. However, it's important to note that what we develop here in this chapter won't yet be a complete, functioning program. For the moment, I invite you to trust in the learning process, understanding that the functions we mention without providing explicit code will be thoroughly explained as we progress.
Remember, this lesson bears the title "Raytracing in a Nutshell." In subsequent lessons, we'll delve into greater detail on each technique introduced, progressively enhancing our understanding and our ability to simulate light and shadow through computation. Nevertheless, by the end of this lesson, you'll have crafted a functional ray tracer capable of compiling and generating images. This marks not just a significant milestone in your learning journey but also a testament to the power and elegance of ray tracing in generating images. Let's go.
Consider the natural propagation of light: a myriad of rays emitted from various light sources, meandering until they converge upon the eye's surface. Ray tracing, in its essence, mirrors this natural phenomenon, albeit in reverse, rendering it a virtually flawless simulator of reality.
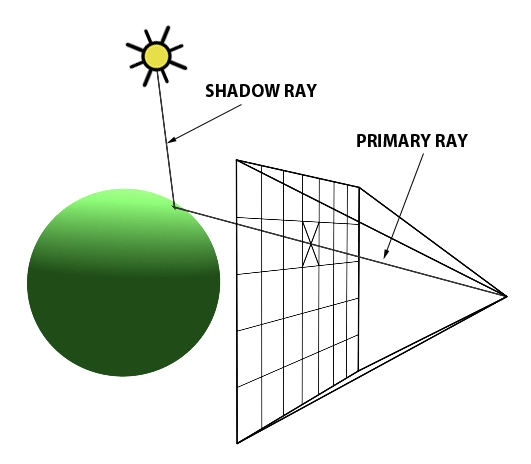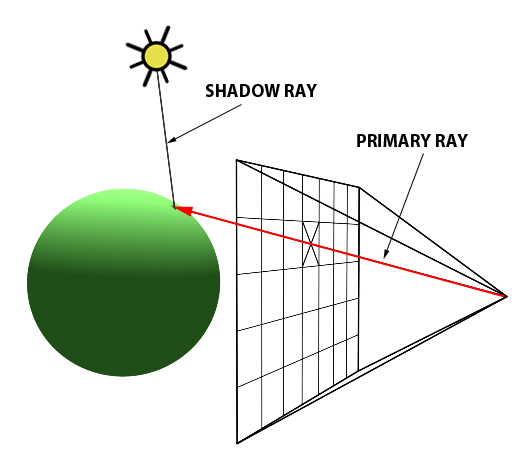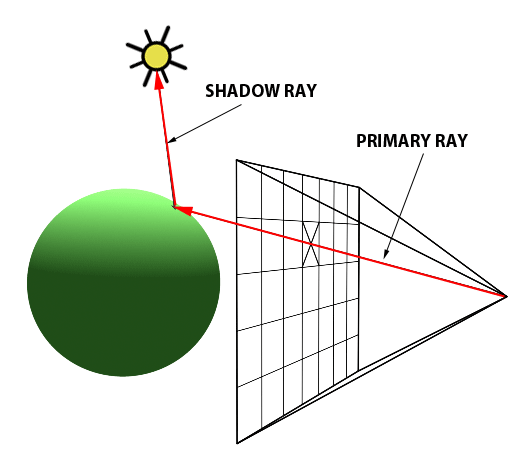
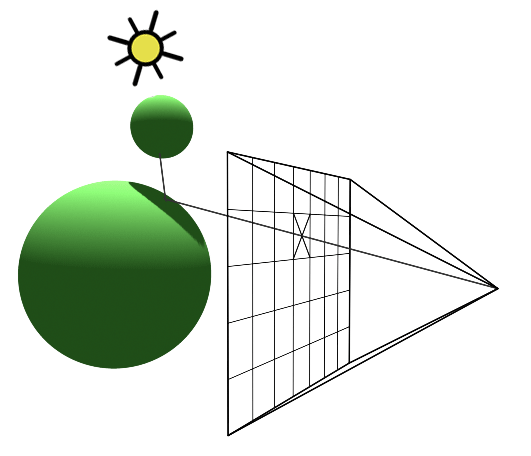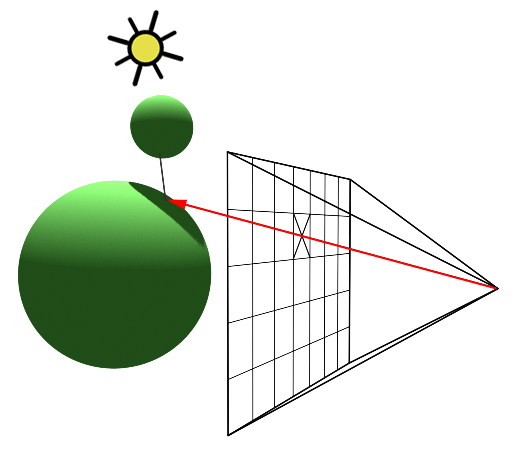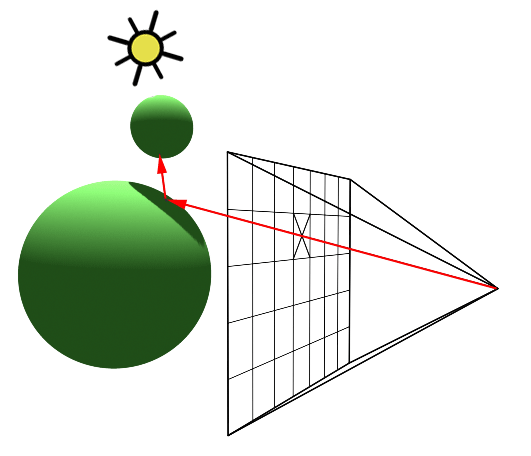
The essence of the ray-tracing algorithm is to render an image pixel by pixel. For each pixel, it launches a primary ray into the scene, its direction determined by drawing a line from the eye through the pixel's center. This primary ray's journey is then tracked to ascertain if it intersects with any scene objects. In scenarios where multiple intersections occur, the algorithm selects the intersection nearest to the eye for further processing. A secondary ray, known as a shadow ray, is then projected from this nearest intersection point towards the light source (Figure 1).
An intersection point is deemed illuminated if the shadow ray reaches the light source unobstructed. Conversely, if it intersects another object en route, it signifies the casting of a shadow on the initial point (Figure 2).
Repeating this procedure across all pixels yields a two-dimensional depiction of our three-dimensional scene (Figure 3).

Below is the pseudocode for implementing this algorithm:
for (int j = 0; j < imageHeight; ++j) {
for (int i = 0; i < imageWidth; ++i) {
// Determine the direction of the primary ray
Ray primRay;
computePrimRay(i, j, &primRay);
// Initiate a search for intersections within the scene
Point pHit;
Normal nHit;
float minDist = INFINITY;
Object *object = NULL;
for (int k = 0; k < objects.size(); ++k) {
if (Intersect(objects[k], primRay, &pHit, &nHit)) {
float distance = Distance(eyePosition, pHit);
if (distance < minDist) {
object = &objects[k];
minDist = distance; // Update the minimum distance
}
}
}
if (object != NULL) {
// Illuminate the intersection point
Ray shadowRay;
shadowRay.direction = lightPosition - pHit;
bool isInShadow = false;
for (int k = 0; k < objects.size(); ++k) {
if (Intersect(objects[k], shadowRay)) {
isInShadow = true;
break;
}
}
}
if (!isInShadow)
pixels[i][j] = object->color * light.brightness;
else
pixels[i][j] = 0;
}
}
The elegance of ray tracing lies in its simplicity and direct correlation with the physical world, allowing for the creation of a basic ray tracer in as few as 200 lines of code. This simplicity contrasts sharply with more complex algorithms, like scanline rendering, making ray tracing comparatively effortless to implement.
Arthur Appel first introduced ray tracing in his 1969 paper, "Some Techniques for Shading Machine Renderings of Solids". Given its numerous advantages, one might wonder why ray tracing hasn't completely supplanted other rendering techniques. The primary hindrance, both historically and to some extent currently, is its computational speed. As Appel noted:
This method is very time consuming, usually requiring several thousand times as much calculation time for beneficial results as a wireframe drawing. About one-half of this time is devoted to determining the point-to-point correspondence of the projection and the scene.
Thus, the crux of the issue with ray tracing is its slowness—a sentiment echoed by James Kajiya, a pivotal figure in computer graphics, who remarked, "ray tracing is not slow - computers are". The challenge lies in the extensive computation required to calculate ray-geometry intersections. For years, this computational demand was the primary drawback of ray tracing. However, with the continual advancement of computing power, this limitation is becoming increasingly mitigated. Although ray tracing remains slower compared to methods like z-buffer algorithms, modern computers can now render frames in minutes that previously took hours. The development of real-time and interactive ray tracing is currently a vibrant area of research.
In summary, ray tracing's rendering process can be bifurcated into visibility determination and shading, both of which necessitate computationally intensive ray-geometry intersection tests. This method offers a trade-off between rendering speed and accuracy. Since Appel's seminal work, extensive research has been conducted to expedite ray-object intersection calculations. With these advancements and the rise in computing power, ray tracing has emerged as a standard in offline rendering software. While rasterization algorithms continue to dominate video game engines, the advent of GPU-accelerated ray tracing and RTX technology in 2017-2018 marks a significant milestone towards real-time ray tracing. Some video games now feature options to enable ray tracing, albeit for limited effects like enhanced reflections and shadows, heralding a new era in gaming graphics.