The Raytracing Algorithm in a Nutshell
Reading time: 8 mins.Ibn al-Haytham's work sheds light on the fundamental principles behind our ability to see objects. From his studies, two key observations emerge: first, without light, visibility is null, and second, without objects to interact with, light itself remains invisible to us. This becomes evident in scenarios such as traveling through intergalactic space, where the absence of matter results in nothing but darkness, despite the potential presence of photons traversing the void (assuming photons are present, they must originate from a source, and seeing them would involve their direct interaction with our eyes, revealing the source from which they were reflected or emitted).
Forward Tracing
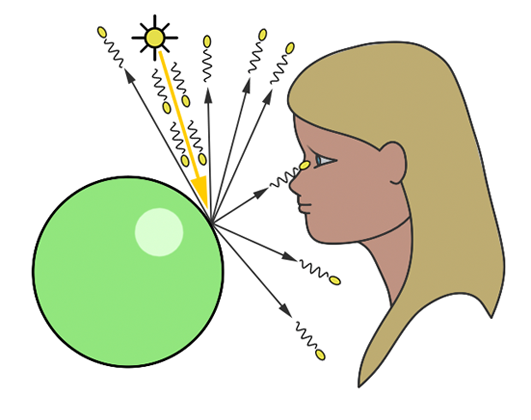
In the context of simulating the interaction between light and objects in computer graphics, it's crucial to understand another physical concept. Of the myriad rays reflected off an object, only a minuscule fraction will actually be perceived by the human eye. For instance, consider a hypothetical light source designed to emit a single photon at a time. When this photon is released, it travels in a straight line until it encounters an object's surface. Assuming no absorption, the photon is then reflected in a seemingly random direction. If this photon reaches our eye, we discern the point of its reflection on the object (as illustrated in figure 1).
You've stated previously that "each point on an illuminated object disperses light rays in all directions." How does this align with the notion of 'random' reflection?
The comprehensive explanation for light's omnidirectional reflection from surfaces falls outside this lesson's scope (for a detailed discussion, refer to the lesson on light-matter interaction). To succinctly address your query: it's both yes and no. Naturally, a photon's reflection off a surface follows a specific direction, determined by the surface's microstructure and the photon's approach angle. Although an object's surface may appear uniformly smooth to the naked eye, microscopic examination reveals a complex topography. The accompanying image illustrates paper under varying magnifications, highlighting this microstructure. Given photons' diminutive scale, they are reflected by the myriad micro-features on a surface. When a light beam contacts a diffuse object, the photons encounter diverse parts of this microstructure, scattering in numerous directions—so many, in fact, that it simulates reflection in "every conceivable direction." In simulations of photon-surface interactions, rays are cast in random directions, which statistically mirrors the effect of omnidirectional reflection.
Certain materials exhibit organized macrostructures that guide light reflection in specific directions, a phenomenon known as anisotropic reflection. This, along with other unique optical effects like iridescence seen in butterfly wings, stems from the material's macroscopic structure and will be explored in detail in lessons on light-material interactions.

In the realm of computer graphics, we substitute our eyes with an image plane made up of pixels. Here, photons emitted by a light source impact the pixels on this plane, incrementally brightening them. This process continues until all pixels have been appropriately adjusted, culminating in the creation of a computer-generated image. This method is referred to as forward ray tracing, tracing the path of photons from their source to the observer.
Yet, this approach raises a significant issue:
In our scenario, we assumed that every reflected photon would intersect with the eye's surface. However, given that rays scatter in all possible directions, each has a minuscule chance of actually reaching the eye. To encounter just one photon that hits the eye, an astronomical number of photons would need to be emitted from the light source. This mirrors the natural world, where countless photons move in all directions at the speed of light. For computational purposes, simulating such an extensive interaction between photons and objects in a scene is impractical, as we will soon elaborate.
One might ponder: "Should we not direct photons towards the eye, knowing its location, to ascertain which pixel they intersect, if any?" This could serve as an optimization for certain material types. We'll later delve into how diffuse surfaces, which reflect photons in all directions within a hemisphere around the contact point's normal, don't require directional precision. However, for mirror-like surfaces that reflect rays in a precise, mirrored direction (a computation we'll explore later), arbitrarily altering the photon's direction is not viable, making this solution less than ideal.
Is the eye merely a point receptor, or does it possess a surface area? Even if small, the receiving surface is larger than a point, thus capable of capturing more than a singular ray out of zillions.
Indeed, the eye functions more like a surface receptor, akin to the film or CCD in cameras, rather than a mere point receptor. This introduction to the ray-tracing algorithm doesn't delve deeply into this aspect. Cameras and eyes alike utilize a lens to focus reflected light onto a surface. Should the lens be extremely small (unlike actuality), reflected light from an object would be confined to a single direction, reminiscent of pinhole cameras' operation, a topic for future discussion.
Even adopting this approach for scenes composed solely of diffuse objects presents challenges. Visualize directing photons from a light source into a scene as akin to spraying paint particles onto an object's surface. Insufficient spray density results in uneven illumination.
Consider the analogy of attempting to paint a teapot by dotting a black sheet of paper with a white marker, with each dot representing a photon. Initially, only a sparse number of photons intersect the teapot, leaving vast areas unmarked. Increasing the dots gradually fills in the gaps, making the teapot progressively more discernible.

However, deploying even thousands or multiples thereof of photons cannot guarantee complete coverage of the object's surface. This method's inherent flaw necessitates running the program until we subjectively deem enough photons have been applied to accurately depict the object. This process, requiring constant monitoring of the rendering process, is impractical in a production setting. The primary cost in ray tracing lies in detecting ray-geometry intersections, not in generating photons, but in identifying all their intersections within the scene, which is exceedingly resource-intensive.
Conclusion: Forward ray tracing or light tracing, which involves casting rays from the light source, can theoretically replicate natural light behavior on a computer. However, as discussed, this technique is neither efficient nor practical for actual use. Turner Whitted, a pioneer in computer graphics research, critiqued this method in his seminal 1980 paper, "An Improved Illumination Model for Shaded Display", noting:
In an evident approach to ray tracing, light rays emanating from a source are traced through their paths until they strike the viewer. Since only a few will reach the viewer, this approach could be better. In a second approach suggested by Appel, rays are traced in the opposite direction, from the viewer to the objects in the scene.
Let's explore this alternative strategy Whitted mentions.
Backward Tracing

In contrast to the natural process where rays emanate from the light source to the receptor (like our eyes), backward tracing reverses this flow by initiating rays from the receptor towards the objects. This technique, known as backward ray-tracing or eye tracing because rays commence from the eye's position (as depicted in figure 2), effectively addresses the limitations of forward ray tracing. Given the impracticality of mirroring nature's efficiency and perfection in simulations, we adopt a compromise by casting a ray from the eye into the scene. Upon impacting an object, we evaluate the light it receives by dispatching another ray—termed a light or shadow ray—from the contact point towards the light source. If this "light ray" encounters obstruction by another object, it indicates that the initial point of contact is shadowed, receiving no light. Hence, these rays are more aptly called shadow rays. The inaugural ray shot from the eye (or camera) into the scene is referred to in computer graphics literature as a primary ray, visibility ray, or camera ray.
Throughout this lesson, forward tracing is used to describe the method of casting rays from the light, in contrast to backward tracing, where rays are projected from the camera. Nonetheless, some authors invert these terminologies, with forward tracing denoting rays emitted from the camera due to its prevalence in CG path-tracing techniques. To circumvent confusion, the explicit terms of light and eye tracing can be employed, particularly within discussions on bi-directional path tracing (refer to the Light Transport section for more).
Conclusion
The technique of initiating rays either from the light source or from the eye is encapsulated by the term path tracing in computer graphics. While ray-tracing is a synonymous term, path tracing emphasizes the methodological essence of generating computer-generated imagery by tracing the journey of light from its source to the camera, or vice versa. This approach facilitates the realistic simulation of optical phenomena such as caustics or indirect illumination, where light reflects off surfaces within the scene. These subjects are slated for exploration in forthcoming lessons.