Light Transport
Reading time: 22 mins.It's neither simple nor complicated, but it is often misunderstood.
Light Transport
In a typical scene, light is likely to bounce off of the surface of many objects before it reaches the eye. As explained in the previous chapter, the direction in which light is reflected depends on the material type (is it diffuse, specular, etc.), thus light paths are defined by all the successive materials the light rays interact with on their way to the eye.
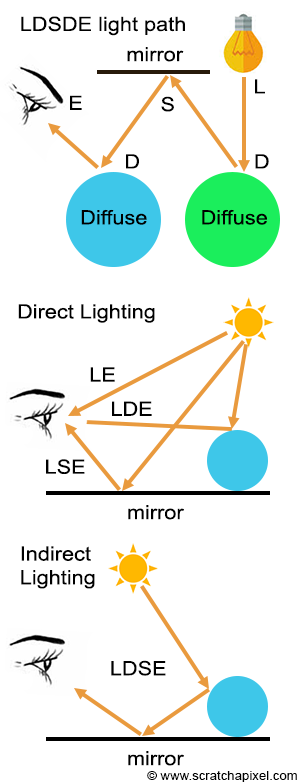
Imagine a light ray emitted from a light source, reflected off of a diffuse surface, then a mirror surface, then a diffuse surface again and then reaching the eye. If we label, the light L, the diffuse surface D, the specular surface S (a mirror reflection can be seen as an ideal specular reflection, one in which the roughness of the surface is 0) and the eye E, the light path in this particular example is LDSDE. Of course, you can imagine all sorts of possible combinations; this path can even be an "infinitely" long string of Ds and Ss. The one thing that all these rays will have in common, is an L at the start and an E at the end. The shortest possible light path is LE (you look directly at something that emits light). If light rays bounce off the surface only once, which using the light path notation could be expressed as either LSE or LDE, then we have a case of direct lighting (direct specular or direct diffuse). Direct specular is what you have when the sun is reflected off of a water surface for instance. If you look at the reflection of a mountain in the lake, you are more likely to have an LDSE path (assuming the mountain is a diffuse surface), etc. In this case, we speak of indirect lighting.
Researcher Paul Heckbert introduced the concept of labeling paths that way in a paper published in 1990 and entitled "Adaptive Radiosity Textures for Bidirectional Ray Tracing". It is not uncommon to use regular expressions to describe light paths compactly. For example, any combination of reflection off the surface of a diffuse or specular surface can be written as: L(D|S)*E. In Regex (the abbreviation for regular expression), (a|b)* denotes the set of all strings with no symbols other than "a" and "b", including the empty string: {"", "a", "b", "aa", "ab", "ba", "bb", "aaa", ...}.
At this point, you may think, "this is all good, but how does that relate to rendering?". As mentioned several times already in this lesson and the previous one, in the real world, light goes from light sources to the eye. But only a fraction of the rays emitted by light sources reaches the eye. Therefore, rather than simulating light path from the source to the eye, a more efficient approach is to start from the eye, and walk back to the source.
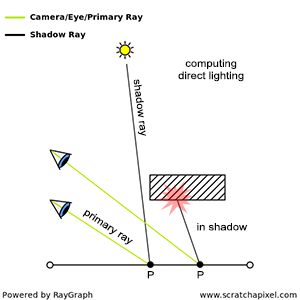
This is what we typically do in ray tracing. We trace a ray from the eye (we generally call the eye ray, primary ray, or camera ray) and check whether this ray intersects any geometry in the scene. If it does (let's call P, the point where the ray intersects the surface), we then need to do two things: compute how much light arrives at P from the light sources (direct lighting), and how much light arrives at P indirectly, as a result of light being reflected by other surfaces in the scene (indirect lighting).
-
To compute the direct contribution of light to the illumination of P, we trace a ray from P to the source. If this ray intersects another object on its way to the light, then P is in the shadow of this light (which is why we sometimes call these rays shadow rays). This is illustrated in figure 2.
-
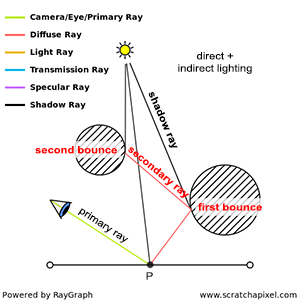
Indirect lighting comes from other objects in the scene reflecting light towards P, whether as a result of these objects reflecting light from a light source or as a result of these objects reflecting light which is itself bouncing off of the surface of other objects in the scene. In ray tracing, indirect illumination is computed by spawning new rays, called secondary rays from P into the scene (figure 3). Let's explain in more detail how and why this works.
If these secondary rays intersect other objects or surfaces in the scene, then it is reasonable to assume, that light travels along these rays from the surfaces they intersect to P. We know that the amount of light reflected by a surface depends on the amount of light arriving on the surface as well as the viewing direction. Thus to know how much light is reflected towards P along any of these secondary rays, we need to:
-
Compute the amount of light arriving at the point of intersection between the secondary ray and the surface.
-
Measure how much of that light is reflected by that surface to P, using the secondary ray direction as our viewing direction.
Remember that specular reflection is view-dependent: how much light is reflected by a specular surface depends on the direction from which you are looking at the reflection. Diffuse reflection though is view-independent: the amount of light reflected by a diffuse surface doesn't change with direction. Thus unless diffuse, a surface doesn't reflect light equally in all directions.
Computing how much light arrives at a point of intersection between a secondary ray and a surface, is no different than computing how much light arrives at P. Computing how much light is reflected in the ray direction towards P, depends on the surface properties, and is generally done in what we call a shader. We will talk about shaders in the next chapter.
Other surfaces in the scene potentially reflect light to P. We don't know which one and light can come from all possible directions above the surface at P (light can also come from underneath the surface if the object is transparent or translucent -- but we will ignore this case for now). However, because we can't test every single possible direction (it would take too long) we will only test a few directions instead. The principle is the same as when you want to measure for instance the average height of the adult population of a given country. There might be too many people in this population to compute that number exactly, however, you can take a sample of that population, let's say maybe a few hundreds or thousands of individuals, measure their height, make an average (sum up all the numbers and divide by the size of your sample), and get that way, an approximation of the actual average adult height of the entire population. It's only an approximation, but hopefully, it should be close enough to the real number (the bigger the sample, the closer the approximation to the exact solution). We do the same thing in rendering. We only sample a few directions and assume that their average result, is a good approximation of the actual solution. If you heard about the term Monte Carlo before and particularly Monte Carlo ray tracing, that's what this technique is all about. Shooting a few rays to approximate the exact amount of light arriving at a point. The downside is that the result is only an approximation. The bright side is that we get a result for a problem that is otherwise not tractable (e.i. it is impossible to compute exactly within any amount of reasonable finite time).
Computing indirect illumination is a recursive process. Secondary rays are generated from P, which in turn generate new intersection points, from which other secondary rays are generated, and so on. We can count the number of times light is reflected from surfaces from the light source until it reaches P. If light bounces off the surface of objects only once before it gets to P we have... one bounce of indirect illumination. Two bounces, light bounces off twice, three bounces, three times, etc.
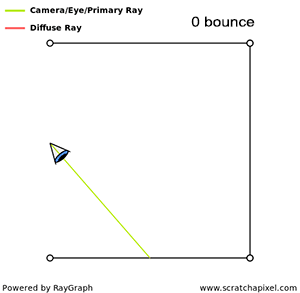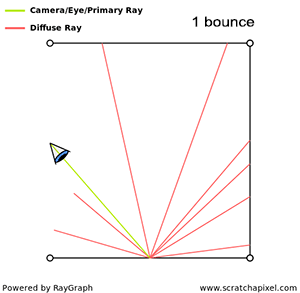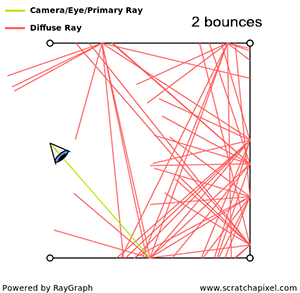
The number of times light bounces off the surface of objects can be infinite (imagine a situation for example in which a camera is inside a box illuminated by a light on the ceiling? rays would keep bouncing off the walls forever). To avoid this situation, we generally stop spawning secondary rays after a certain number of bounces (typically 1, 2, or 3). Note though that as a result of setting a limit to the number of bounces, P is likely to look darker than it actually should (since any fraction of the total amount of light emitted by a light source that took more bounces than the limit to arrive at P, will be ignored). If we set the limit to two bounces for instance, then we ignore the contribution of all the other bounces above (third, fourth, etc.). However luckily enough, each time light bounces off of the surface of an object, it loses a little bit of its energy. This means that as the number of bounces increases, the contribution of these bounces to the indirect illumination of a point decreases. Thus, there is a point after which you might consider that computing one more bounce makes such a little difference to the image, that it doesn't justify the amount of time it takes to simulate it.
If we decide, for example, to spawn 32 rays each time we intersect a surface to compute the amount of indirect lighting (and assuming each one of these rays intersects a surface in the scene), then on our first bounce we have 32 secondary rays. Each one of these secondary rays generates another 32 secondary rays. Which makes already a total of 1024 rays. After three bounces we generated a total of 32768 rays! If ray tracing is used to compute indirect lighting, it generally becomes quickly very expensive because the number of rays grows exponentially as the number of bounces increases. This is often referred to as the curse of ray tracing.
Figure 5: when we compute direct lighting, we need to cast a shadow ray from the point where the primary ray intersected geometry to each light source in the scene. If this shadow ray intersects another object "on its way to the light source", then this point is in shadow.
This long explanation is to show you, that the principle of actually computing the amount of light impinging upon P whether directly or indirectly is simple, especially if we use the ray-tracing approach. The only sacrifice to physical accuracy we made so far, is to put a cap on the maximum number of bounces we compute, which is necessary to ensure that the simulation will not run forever. In computer graphics, this algorithm is known as unidirectional path tracing (it belongs to a larger category of light transport algorithms known as path tracing). This is the simplest and most basic of all light transport models based on ray tracing (it also goes by the name of classic ray tracing or Whitted style ray tracing). It's called unidirectional, because it only goes in one direction, from the eye to the light source. The part "path tracing" is pretty straightforward: it's all about tracing light paths through the scene.
Classic ray tracing generates a picture by tracing rays from the eye into the scene, recursively exploring specularly reflected and transmitted directions, and tracing rays toward point light sources to simulate shadows. (Paul S. Heckbert - 1990 in "Adaptive Radiosity Textures for Bidirectional Ray Tracing")
This method was originally proposed by Appel in 1986 ("Some Techniques for Shading Machine Rendering of Solids") and later developed by Whitted (An improved illumination model for shaded display - 1979).
When the algorithm was first developed, Appel and Whitted only considered the case of mirror surfaces and transparent objects. This is only because computing secondary rays (indirect lighting) for these materials require fewer rays than for diffuse surfaces. To compute the indirect reflection of a mirror surface, you only need to cast one single reflection ray into the scene. If the object is transparent, you need to cast one ray for the reflection and one ray for the refraction. However, when the surface is diffuse, to approximate the amount of indirect lighting at P, you need to cast many more rays (typically 16, 32, 64, 128 up to 1024 - this number though doesn't have a power of 2 but it usually is for reasons will explain in due time) distributed over the hemisphere oriented about the normal at the point of incidence. This is far more costly than just computing reflection and refraction (either one or two rays per shaded point), so their first developed their concept by using specular and transparent surfaces to start with as computers back then were very slow compared to today's standards; but extending their algorithm to indirect diffuse was, of course, straightforward.
Other techniques than ray tracing can be used to compute global illumination. Note though that ray tracing seems to be the most adequate way of simulating the way light spreads out in the real world. But things are not that simple. With unidirectional path tracing, for example, some light paths are more complicated to compute efficiently than others. This is particularly true of light paths involving specular surfaces illuminating diffuse surfaces (or any type of surfaces for that matter) indirectly. Let's take an example.
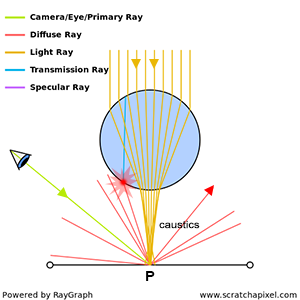
As you can see in the image above, in this particular situation, light emitted by the source at the top of the image, is refracted through a (transparent) glass ball which by the effect of refraction, concentrates all light rays towards a singular point on the plane underneath. This is what we call a caustic. Note that, no direct light arrives at P from the light source directly (P is in the 'shadow' of the sphere). It all comes indirectly through the sphere by the mean of refraction and transmission. While it may seem more natural in this particular situation to trace light from the light source to the eye, considering that we decided to trace light rays the other way around, let's see what we get.
When it will come to computing how much light arrives at P indirectly if we assume that the surface at P is diffuse, then we will spawn a bunch of rays in random directions to check which surfaces in the scene redirect light towards P. But by doing so, we will fail to account for the fact that all light comes from the bottom surface of the sphere. So obviously we could maybe solve this problem by spawning all rays from P toward the sphere, but since our approach assumes we have no prior knowledge of how light travels from the light source to every single point in the scene, that's not something we can do (we have no prior knowledge that a light source is above the sphere and no reason to assume that this light is the light that contributes to the illumination of P via transmission and refraction). All we can do is spawn rays in random directions as we do with all other surfaces, which is how unidirectional path tracing works. One of these rays might actually hit the sphere and get traced back to the light source (but we don't even have a guarantee that even a single ray will hit the sphere since their directions are chosen randomly), however, this might only be one ray over maybe 10 or 20 or 100 we cast into the scene, thus we might miserably fail in this particular case to compute how much light arrives at P indirectly.
Isn't 1 ray over 10 or 20 enough? Yes and no. It's hard to explain the technique used here to "approximate" the indirect lighting component of the illumination of P but in short, it's based on probabilities and is very similar in a way to measuring an "approximation" of a given variable using a poll. For example, when you want to measure the average height of the adult population of a given country, you can't measure the height of every person making up that population. Instead, you just take a sample, a subset of that population, measure the average height of that sample and assume that this number is close enough to the actual average height of the entire population. While the theory behind this technique is not that simple (you need to prove that this approach is mathematically correct and not purely empirical), the concept is pretty simple to understand. We do the same thing here to approximate the indirect lighting component. We chose random directions, measure the amount of light coming from these directions, average the result, and assume the resulting number is an "approximation" of the actual amount of indirect light received by P. This technique is called Monte Carlo integration. It's a very important method in rendering and you will find it explained in great detail in a couple of lessons from the "Mathematics and Physics of Computer Graphics" section. If you want to understand why 1 ray over 20 secondary rays is not ideal in this particular case, you will need to read these lessons.
Using Heckbert light path's naming convention, we can say that paths of the kind LS+DE are generally hard to simulate in computer graphics using the basic approach of tracing back the path of light rays from the eye to the source (or unidirectional path tracing). In Regex, the + sign account for any sequences that match the element preceding the sign one or more times. For example, ab+c matches "abc", "abbc", "abbbc", and so on, but not "ac". What this means in our case, is that situations in which light is reflected off of the surface of one or more specular surfaces before it reaches a diffuse surface and then the eye (as in the example of the glass sphere), are hard to simulate using unidirectional path tracing.
What do we do then? This is where the art of light transport comes into play.
While being simple and thus very appealing for this reason, a naive implementation of tracing light paths to the eye is not efficient in some cases. It seems to work well when the scene is only made of diffuse surfaces but is problematic when the scene contains a mix of diffuse and specular surfaces (which is more often the case than not). So what do we do? Well, we do the same thing as we usually do when we have a problem. We search for a solution. And in this particular case, this leads to looking for developing strategies (or algorithms) that would work well to simulate all sorts of possible combinations of materials. We want a strategy in which LS+DE paths can be simulated as efficiently as LD+E paths. And since our default strategy doesn't work well in this case, we need to come up with new ones. This led obviously to the development of new light transport algorithms that are better than unidirectional path tracing to solve this light transport problem. More formally light transport algorithms are strategies (implemented in the form of algorithms) that attempt to propose a solution to the problem we just presented: solving efficiently any combination of any possible light path, or more generally light transport.
Light transport algorithms are not that many, but still, quite a few exist. And don't be misled. Nothing in the rules of coming up with the greatest light transport algorithm of all times, tells you that you have to use ray tracing to solve the problem. You have the choice of weapon. Many solutions use what we call a hybrid or multi-passes approach. Photon mapping is an example of such an algorithm. They require the pre-computation of some lighting information stored in specific data structures (a photon map or a point cloud generally for example), before actually rendering the final image. Difficult light paths are resolved more efficiently by taking advantage of the information stored in these structures. Remember that we said in the glass sphere example that we had no prior knowledge of the existence of the light above the sphere? Well, photon maps are a way of looking at the scene before it gets rendered and trying to get some prior knowledge about where light "photons" go before rendering the final image. It is based on that idea.
While being quite popular some years ago, these algorithms though are based on a multi-pass approach. In other words, you need to generate some extra data before you can render your final image. This is great if it helps to render images you couldn't render otherwise, but multi-passes rendering is a pain to manage, requires a lot of extra work, requires generally to store extra data on disk, and the process of actually rendering the image doesn't start before all the pre-computation steps are complete (thus you need to wait for a while before you can see something). As we said, for a long time they were popular because they made it possible to render things such as caustics which would have been too long to render with pure ray tracing, and that therefore, we generally ignored altogether. Thus having a technique to simulate them (no matter how painful it is to set up) is better than nothing. However, of course, a unified approach is better: one in which the multi-pass is not required and one which integrates smoothly with your existing framework. For example, if you use ray tracing (as your framework), wouldn't it be great to come up with an algorithm that only uses ray tracing, and never have to pre-compute anything? Well, it does exist.
Several algorithms have been developed around ray tracing and ray tracing only. Extending the concept of unidirectional path tracing, which we talked about above, we can use another algorithm known as bi-directional path tracing. It is based on the relatively simple idea, that for every ray you spawn from the eye into the scene, you can also spawn a ray from a light source into the scene, and then try to connect their respective paths through various strategies. An entire section of Scratchapixel is devoted to light transport and we will review in this section, some of the most important light transport algorithms, such as unidirectional path tracing, bi-directional path tracing, Metropolis light transport, instant radiosity, photon mapping, radiosity caching, etc.
Summary
Probably one of the most common myths in computer graphics is that ray tracing is both the ultimate and only way to solve global illumination. While it may be the ultimate way in the sense that it offers a much more natural way of thinking about the way light travels in the real world, it also has its limitations, as we showed in this introduction, and it is certainly not the only way. You can broadly distinguish between two sorts of light transport algorithms:
-
Those who are not using ray tracing such as photon or shadow mapping, radiosity, etc.
-
Those who are using ray tracing and ray tracing only.
As long as the algorithm efficiently captures light paths that are difficult to capture with the traditional unidirectional path tracing algorithm, it can be viewed as one of the contendors to solve our LS+DE problem.
Modern implementations do tend to favor the light transport method solely based on ray tracing, simply because ray tracing is a more natural way to think about light propagation in a scene, and offers a unified approach to computing global illumination (one in which using auxiliary structures or systems to store light information is not necessary). Note though that while such algorithms do tend to be the norm these days in off-line rendering, real-time rendering systems are still very much based on the former approach (they are generally not designed to use ray tracing, and still rely on things such as shadow maps or light fields to compute direct and indirect illumination).