Rendering an Image of a 3D Scene: an Overview

It All Starts with a Computer and a Computer Screen

Introduction

The lesson Introduction to Raytracing: A Simple Method for Creating 3D Images provided you with a quick introduction to some important concepts in rendering and computer graphics in general, as well as the source code of a small ray tracer (with which we rendered a scene containing a few spheres). Ray tracing is a very popular technique for rendering a 3D scene (mostly because it is easy to implement and also a more natural way of thinking of the way light propagates in space, as quickly explained in lesson 1), however other methods exist. In this lesson, we will look at what rendering means, what sort of problems we need to solve to render an image of a 3D scene as well as quickly review the most important techniques that were developed to solve these problems specifically; our studies will be focused on the ray tracing and rasterization method, two popular algorithms used to solve the visibility problem (finding out which objects making up the scene is visible through the camera). We will also look at shading, the step in which the appearance of the objects as well as their brightness is defined.

It All Start with a Computer (and a Computer Screen)

The journey in the world of computer graphics starts... with a computer. It might sound strange to start this lesson by stating what may seem obvious to you, but it is so obvious that we do take this for granted and never think of what it means when it comes to making images with a computer. More than a computer, what we should be concerned about is how we display images with a computer: the computer screen. Both the computer and the computer screen have something important in common. They work with discrete structures to the contrary of the world around us, which is made of continuous structures (at least at the macroscopic level). These discrete structures are the bit for the computer and the pixel for the screen. Let's take a simple example. Take a thread in the real world. It is indivisible. But the representation of this thread onto the surface of a computer screen requires to "cut" or "break" it down into small pieces called pixels. This idea is illustrated in figure 1.

In computing, the process of actually converting any continuous object (a continuous function in mathematics, a digital image of a thread) is called discretization. Obvious? Yes and yet, most problems if not all problems in computer graphics come from the very nature of the technology a computer is based on: 0, 1, and pixels.

You may still think "who cares?". For someone watching a video on a computer, it's probably not very important indeed. But if you have to create this video, this is probably something you should care about. Think about this. Let's imagine we need to represent a sphere on the surface of a computer screen. Let's look at a sphere and apply a grid on top of it. The grid represents the pixels your screen is made of (figure 2). The sphere overlaps some of the pixels completely. Some of the pixels are also empty. However, some of the pixels have a problem. The sphere overlaps them only partially. In this particular case, what should we fill the pixel with: the color of the background or the color of the object?

Intuitively you might think "if the background occupies 35% of the pixel area, and the object 75%, let's assign a color to the pixel which is composed of the background color for 35% and of the object color for 75%". This is pretty good reasoning, but in fact, you just moved the problem around. How do you compute these areas in the first place anyway? One possible solution to this problem is to subdivide the pixel into sub-pixels and count the number of sub-pixels the background overlaps and assume all over sub-pixels are overlapped by the object. The area covered by the background can be computed by taking the number of sub-pixels overlapped by the background over the total number of sub-pixels.

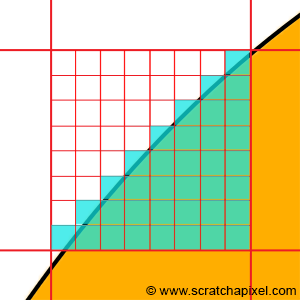
However, no matter how small the sub-pixels are, there will always be some of them overlapping both the background and the object. While you might get a pretty good approximation of the object and background coverage that way (the smaller the sub-pixels the better the approximation), it will always just be an approximation. Computers can only approximate. Different techniques can be used to compute this approximation (subdividing the pixel into sub-pixels is just one of them), but what we need to remember from this example, is that a lot of the problems we will have to solve in computer sciences and computer graphics, comes from having to "simulate" the world which is made of continuous structures with discrete structures. And having to go from one to the other raises all sorts of complex problems (or maybe simple in their comprehension, but complex in their resolution).

Another way of solving this problem is also obviously to increase the resolution of the image. In other words, to represent the same shape (the sphere) using more pixels. However, even then, we are limited by the resolution of the screen.

Images and screens using a two-dimensional array of pixels to represent or display images are called raster graphics and raster displays respectively. The term raster more generally defines a grid of x and y coordinates on a display space. We will learn more about rasterization, in the chapter on perspective projection.

As suggested, the main issue with representing images of objects with a computer is that the object shapes need to be "broken" down into discrete surfaces, the pixels. Computers more generally can only deal with discrete data, but more importantly, the definition with which numbers can be defined in the memory of the computer is limited by the number of bits used to encode these numbers. The number of colors for example that you can display on a screen is limited by the number of bits used to encode RGB values. In the early days of computers, a single bit was used to encode the "brightness" of pixels on the screen. When the bit had the value 0 the pixel was black and when it was 1, the pixel would be white. The first generation of computers used color displays, encoded color using a single byte or 8 bits. With 8 bits (3 bits for the red channel, 3 bits for the green channel, and 2 bits for the blue channel) you can only define 256 distinct colors (2^3 * 2^3 * 2^2). What happens then when you want to display a color which is not one of the colors you can use? The solution is to find the closest possible matching color from the palette to the color you ideally want to display and display this matching color instead. This process is called color quantization.

The problem with color quantization is that when we don't have enough colors to accurately sample a continuous gradation of color tones, continuous gradients appear as a series of discrete steps or bands of color. This effect is called banding (it's also known under the term posterization or false contouring).

There's no need to care about banding so much these days (the most common image formats use 32 bits to encode colors. With 32 bits you can display about 16 million distinct colors), however, keep in mind that fundamentally, colors and pretty much any other continuous function that we may need to represent in the memory of a computer, have to be broken down into a series of discrete or single quantum values for which precision is limited by the number of bits used to encode these values.

Finally, having to break down a continuous function into discrete values may lead to what's known in signal processing and computer graphics as aliasing. The main problem with digital images is that the amount of details you can capture depends on the image resolution. The main issue with this is that small details (roughly speaking, details smaller than a pixel) can't be captured by the image accurately. Imagine for example that you want to take a photograph with a digital camera of a teapot that is so far away though that the object is smaller than a pixel in the image (figure 6). A pixel is a discrete structure thus we can only fill it up with a constant color. If in this example, we fill it up with the teapot's color (assuming the teapot has a constant color which is probably not the case if it's shaded), your teapot will only show up as a dot in the image: you failed to capture the teapot's shape (and shading). In reality, aliasing is far more complex than that, but you should know about the term and know for now and should keep in mind that by the very nature of digital images (because pixels are discrete elements), an image of a given resolution can only accurately represent objects of a given size. We will explain what the relationship between the objects size and the image resolution is in the lesson on Aliasing (which you can find in the Mathematics and Physic of Computer Graphics section).

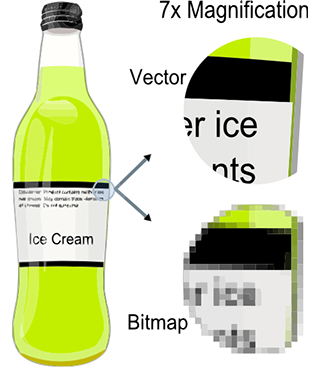
Images are just a collection of pixels. As mentioned before, when an image of the real world is stored in a digital image, shapes are broken down into discrete structures, the pixels. The main drawback of raster images (and raster screens) is that the resolution of the images we can store or display is limited by the image or the screen resolution (its dimension in pixels). Zooming in doesn't reveal more details in the image. Vector graphics were designed to address this issue. With vector graphics, you do not store pixels but represent the shape of objects (and their colors) using mathematical expressions. That way, rather than being limited by the image resolution, the shapes defined in the file can be rendered on the fly at the desired resolution, producing an image of the object's shapes that is always perfectly sharp.

To summarize, computers work with quantum values when in fact, processes from the real world that we want to simulate with computers, are generally (if not always) continuous (at least at the macroscopic and even microscopic scale). And in fact, this is a very fundamental issue that is causing all sorts of very puzzling problems, to which a very large chunk of computer graphics research and theory is devoted.