Rendering an Image of a 3D Scene

Shading

Reading time: 17 mins.

While everything in the real world results from light interacting with matter, some interactions are too complex to simulate using the light transport approach. This is when shading becomes essential.

**Figure 1:** This image shows two objects under the same lighting conditions appearing to have the same color (hue), yet one is darker than the other. This difference in brightness is not due to the amount of light falling on the objects but rather how much light each object reflects into its environment.

As mentioned in the previous chapter, simulating the appearance of an object requires computing the color and brightness of each point on the object's surface. Color and brightness are closely related. It's crucial to distinguish between the brightness caused by the amount of light falling on an object's surface and the brightness of an object's color (sometimes referred to as the color's luminance). The brightness of color, along with its hue and saturation, is a property of color itself. If you observe two objects under identical lighting conditions and they seem to have the same color (same chromaticity), but one is darker than the other, it indicates that their brightness is not solely a result of the light they receive. Instead, it depends more on how much light each object reflects into their environment. In essence, these two objects have the same color (chromaticity) but differ in how much light they reflect (or absorb). Therefore, the brightness (or luminance) of their colors varies. In computer graphics, this characteristic color of an object is termed albedo. Objects' albedo can be measured precisely.

Note that an object cannot reflect more light than it receives (unless it emits light, as light sources do). The color of an object, particularly for diffuse surfaces, can generally be calculated as the ratio of reflected light to the amount of incoming (white) light. Since an object cannot reflect more light than it receives, this ratio is always less than 1. Consequently, colors of objects are defined in the RGB system as values between 0 and 1 for floating-point encoding, or 0 and 255 if using a byte. It is more practical to express this ratio as a percentage. For example, if the ratio—also referred to as color or albedo (these terms are interchangeable)—is 0.18, the object reflects 18% of the incoming light back into the environment. Learn more about this topic in the lesson on Colors.

Defining the color of an object as the ratio of the amount of reflected light over the amount of light incident on the surface, as explained previously, means that color cannot exceed one. However, this does not imply that the quantities of incident and reflected light off the surface of an object cannot be greater than one; it is only the ratio between them that cannot exceed one. What we perceive with our eyes is the product of the amount of light incident on a surface and the object's color. For example, if the energy of the light impinging upon the surface is 1000, and the color of the object is 0.5, then the amount of light reflected by the surface to the eye is 500. This simplification is technically incorrect from a physics perspective, but it serves to illustrate the concept. In the lesson on shading and light transport, we will delve into what these values of 1000 or 500 mean in physical units and understand that the interaction is more complex than merely multiplying the number of photons by 0.5 or the albedo of the object.

Thus, assuming we know the color (albedo) of an object, to compute the actual brightness of a point $P$ on the surface of that object under certain lighting conditions (referring to the actual amount of light energy reflected by the surface to the eye, not the brightness or luminance of the object's albedo), we need to consider two factors:

How much light falls on the object at this point?
How much light is reflected from this point in the viewing direction?

It is important to remember that for specular surfaces, the amount of light reflected depends on the viewing angle. Moving around a mirror, for instance, changes the image reflected; the amount of light reflected towards you varies with the viewpoint.

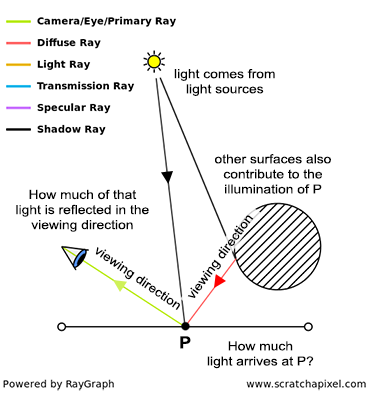
**Figure 2:** To compute the actual brightness of a point $P$ on the surface under certain lighting conditions, we must consider how much light falls on the object at this point and how much light is reflected in the viewing direction. Calculating the light arriving at $P$ involves summing up contributions from light sources (direct lighting) and other surfaces (indirect lighting).

Knowing an object's color (its albedo), we must determine how much light arrives at point $P$ and how much light is reflected in the viewing direction, from $P$ to the eye.

The first task involves "gathering" light at point $P$ above the surface, which is more a light transport issue. As explained in the previous chapter, this can be accomplished by tracing rays directly to lights for direct lighting and spawning secondary rays from $P$ to compute indirect lighting (the contribution of other surfaces to $P$'s illumination). While this might seem solely a light transport problem, forthcoming lessons on Shading and Light Transport will reveal that the surface type (diffuse or specular) dictates the direction of these rays, with shaders playing a critical role in selecting these directions. Furthermore, methods other than ray tracing can be employed to calculate both direct and indirect lighting.
The second task (determining how much light is reflected in a given direction) is significantly more complex and will be explored in greater detail.

First, it's essential to understand that light reflected into the environment by a surface results from complex interactions between light rays (or photons, for those familiar with the term) and the material comprising the object. There are three critical points to note:

These interactions are generally so complex that simulating them directly is impractical.
The amount of light reflected depends on the viewing direction. Generally, surfaces do not reflect incident light equally in all directions. This is not true for perfectly diffuse surfaces, which appear equally bright from all viewing angles, but it does apply to all specular surfaces. Since most objects in the real world exhibit a mix of diffuse and specular reflections, it is more common than not that light is not reflected equally.
The amount of light redirected in the viewing direction also depends on the incoming light's direction. To compute how much light is reflected in the direction $\omega_v$ (where "v" stands for view and $\omega$ is the Greek letter omega), we also need to consider the incoming light direction $\omega_i$ ("i" stands for incident or incoming). This concept is illustrated in Figure 3. Consider what happens when the surface reflecting a ray is a mirror. According to the law of reflection, the angle between the incident direction $\omega_i$ of a light ray and the normal at the point of incidence, and the direction between the reflected or mirror direction $\omega_r$ and the normal, are the same. When the viewing direction $\omega_v$ and the reflected direction $\omega_r$ are the same (Figure 3 - top), the reflected ray enters the eye. However, when $\omega_v$ and $\omega_r$ differ (Figure 3 - bottom), the reflected ray does not travel towards the eye, and thus, it is not visible. Therefore, the amount of light reflected towards the eye depends on both the incident light direction $\omega_i$ and the viewing direction $\omega_v$.

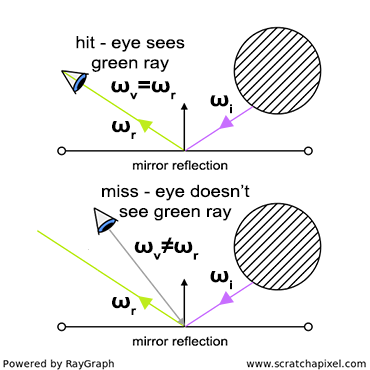
**Figure 3:** For mirror surfaces, if the view direction and the reflected ray direction are not the same, the reflected ray of light is not visible. The amount of light reflected is a function of both the incoming light direction and the viewing direction.

Let's summarize what we know:

Simulating light-matter interactions (happening at the microscopic and atomic levels) is too complex, necessitating alternative solutions.
The amount of light reflected from a point varies with the viewing direction $\omega_v$.
For a given viewing direction $\omega_v$, the amount of light reflected depends on the incoming light direction $\omega_i$.

Shading, which is responsible for computing the amount of light reflected from surfaces to the eye (or other surfaces in the scene), depends on at least two variables: the incident light direction $\omega_i$ and the outgoing or viewing direction $\omega_v$. The origin of light is independent of the surface, but the amount of light reflected in a given direction varies with the surface type (diffuse or specular). As previously mentioned, gathering light at the incident point is more a light transport problem. Regardless of the technique used to gather light at point P, it is crucial to determine the light's origin, i.e., from which direction it comes. A shader takes the incident light direction and the viewing direction as input variables and returns the fraction of light reflected by the surface for these directions.

$$\text{ratio of reflected light} = \text{shader}(\omega_i, \omega_o)$$

Simulating light-matter interactions to obtain a result is complex, but the outcome of these numerous interactions is predictable and consistent, allowing for approximation or modeling with mathematical functions. We will explore the origins, nature, and discovery of these functions in lessons devoted to shading. For now, let's intuit how and why this works.

The law of reflection, introduced in a previous chapter, can be expressed as:

$$\omega_r = \omega_i - 2(N \cdot \omega_i) N$$

In plain English, this equation means that the reflection direction $\omega_r$ can be calculated as $\omega_i$ minus two times the dot product of N (the surface normal at the point of incidence) and $\omega_i$, multiplied by N. This formula relates more to computing a direction than the amount of light reflected. However, if for any given incident direction ($\omega_i$), $\omega_r$ coincides with $\omega_v$ (the viewing direction), then the ratio of reflected light for this particular configuration is 1 (Figure 3 - top). If $\omega_r$ and $\omega_v$ differ, the amount of reflected light would be 0. To formalize this concept, you can write:

$$\text{ratio of reflected light} = \begin{cases} 1 & \text{if } \omega_r = \omega_o \\ 0 & \text{otherwise} \end{cases}$$

This is just an example. For perfectly mirror-like surfaces, we never proceed in this way. The point here is to understand that if we can describe the behavior of light with equations, then we can compute how much light is reflected for any given set of incident and outgoing directions without having to run a complex and time-consuming simulation. This is precisely what shaders do: they replace complex light-matter interactions with a mathematical model, which is fast to compute. These models are not always very accurate or physically plausible, as we will soon see, but they are the most practical way of approximating the results of these interactions. Research in the field of shading primarily involves developing new mathematical models that match as closely as possible the way materials reflect light. As you may imagine, this is a challenging task: it's difficult on its own, but more importantly, materials exhibit very different behaviors, making it generally impossible to simulate accurately all materials with a single model. Instead, it is often necessary to develop one model that works, for example, to simulate the appearance of cotton, another to simulate the appearance of silk, etc.

What about simulating the appearance of a diffuse surface? For diffuse surfaces, we know that light is reflected equally in all directions. The amount of light reflected towards the eye is thus the total amount of light arriving at the surface (at any given point) multiplied by the surface color (the fraction of the total amount of incident light the surface reflects back into the environment), divided by some normalization factor that is necessary for mathematical/physical accuracy reasons. This will be explained in detail in the lessons devoted to shading. Note that for diffuse reflections, the incoming and outgoing light directions do not influence the amount of reflected light. However, this is an exception. For most materials, the amount of reflected light depends on $\omega_i$ and $\omega_v$.

The behavior of glossy surfaces is the most difficult to reproduce with equations. Many solutions have been proposed, the simplest (and easiest to implement in code) being the Phong specular model, which you may have heard about.

The Phong model computes the perfect mirror direction using the equation for the law of reflection, which depends on the surface normal and the incident light direction. It then computes the deviation (or difference) raised to some exponent, between the actual view direction and the mirror direction (by taking the dot product between these two vectors) and assumes that the brightness of the surface at the point of incidence is inversely proportional to this difference. The smaller the difference, the shinier the surface. The exponent parameter helps control the spread of the specular reflection (check the lessons in the Shading section to learn more about the Phong model).

However, good models follow some well-known properties that the Phong model lacks. One of these rules, for instance, is that the model conserves energy. The amount of light reflected in all directions shouldn't be greater than the total amount of incident light. If a model doesn't have this property (the Phong model lacks this property), then it would violate the laws of physics. While it might provide a visually pleasing result, it would not produce a physically plausible one.

Have you already heard the term physically plausible rendering? It designates a rendering system designed around the idea that all shaders and light transport models comply with the laws of physics. In the early days of computer graphics, speed and memory were more important than accuracy, and a model was often considered to be good if it was fast and had a low memory footprint (at the expense of accuracy). But in our quest for photorealism, and because computers are now faster than they were when the first shading models were designed, we don't trade accuracy for speed anymore and use physically-based models wherever possible (even if they are slower than non-physically based models). The conservation of energy is one of the most important properties of a physically-based model. Existing physically based rendering engines can produce images of great realism.

Let's put these ideas together with some pseudo-code:

Vec3f myShader(Vec3f Wi, Vec3f Wo) 
{ 
    // Define the object's color, roughness, etc.
    ... 
    // Do some mathematics to compute the ratio of light reflected
    // by the surface for this pair of directions (incident and outgoing).
    ... 
    return ratio; 
} 
 
Vec3f shadeP(Vec3f ViewDirection, Vec3f Point, Vec3f SurfaceNormal) 
{ 
    Vec3f totalAmountReflected = 0; 
    for (all light sources above P [direct|indirect]) { 
        totalAmountReflected += 
            lightEnergy * 
            shaderDiffuse(LightDirection, ViewDirection) *
            dotProduct(SurfaceNormal, LightDirection); 
    } 
 
    return totalAmountReflected; 
}

Notice how the code is divided into two main sections: a routine (line 11) to gather all light coming from directions above point P, and another routine (line 1), the shader, which computes the fraction of light reflected by the surface for any given pair of incident and viewing directions. The loop, often referred to as a light loop, sums up the contributions from all possible light sources in the scene to the illumination of P. Each light source possesses a certain energy and originates from a specific direction (defined by the line between P and the light source's position in space). All that's needed is to forward this information, along with the viewing direction, to the shader. The shader then calculates the fraction of light from that specific direction that is reflected towards the eye, and this result is multiplied by the amount of light produced by the light source. Summing these results for all possible light sources in the scene yields the total amount of light reflected from P towards the eye, which is the desired outcome.

Note that in the sum (line 18), there is a third term: a dot product between the normal and the light direction. This term is crucial in shading and is related to the cosine law. It will be elaborated on in sections about Light Transport and Shading. For now, it's important to understand that it accounts for the distribution of light energy across the surface of an object as the angle between the surface and the light source changes.

Conclusion

A fine line exists between light transport and shading. As we delve into the section on Light Transport, it becomes clear that light transport algorithms often depend on shaders to determine the direction in which to spawn secondary rays for computing indirect lighting.

Two key takeaways from this chapter include the definitions of shading and shaders:

Shading is the part of the rendering process responsible for computing the amount of light reflected in any given viewing direction. It is at this stage that objects in the image receive their final appearance from a particular viewpoint, including aspects like look, color, texture, and brightness. Simulating an object's appearance boils down to answering a single question: How much light does an object reflect (and in which directions) relative to the total amount it receives?
Shaders are designed to answer this question. Think of a shader as a kind of black box where you pose the question: "Given that this object is made of wood, with a specific color and roughness, and if a certain amount of light strikes this object from direction $\omega_i$, how much light would be reflected by the object back into the environment in direction $\omega_v$?" The shader responds to this query. It is described as a black box not because its internal workings are mysterious, but because it functions as a separate entity within the rendering system. It has a singular purpose—to answer the question posed above—and does so without requiring any knowledge of the system beyond the surface properties (such as roughness and color) and the incoming and outgoing directions.

What happens inside this "black box" is far from mysterious. The unique appearance of objects is the result of complex interactions between light particles (photons) and the atoms that objects are composed of. Although simulating these interactions directly is impractical, we have observed that their outcomes are predictable and consistent. Mathematics can thus be employed to "model" or represent how the real world operates. While a mathematical model is never an exact replica of reality, it serves as a convenient means to express complex problems compactly and can be used to compute solutions (or approximations) to complex issues in a fraction of the time required for direct simulations. The science of shading involves developing such models to describe objects' appearances as a result of light interactions at the micro- and atomic scales. The complexity of these models varies depending on the type of surface appearance we wish to replicate. Simple models exist for perfectly diffuse and mirror-like surfaces, but devising good models for glossy and translucent surfaces poses a much greater challenge.

These models will be examined in the lessons devoted to shading within this section.

Historically, techniques for rendering 3D scenes in real-time were largely predefined by the API, offering little flexibility for users to modify them. Real-time technologies have evolved beyond this paradigm to provide a more programmable pipeline, where each step of the rendering process is controlled by separate "programs" called "shaders." The current OpenGL APIs now support four types of shaders: vertex, geometry, tessellation, and fragment shaders. The shader responsible for computing the color of a point in the image is the fragment shader, while the other shaders play minor roles in defining the object's appearance. It's important to note that the term "shader" has thus come to be used in a broader sense.