Rendering an Image of a 3D Scene: an Overview

And It Follows with a 3D Scene

And It Follows With a 3D Scene

Before we can speak about rendering, we need to consider what we are going to render, and what we are looking at. If you have nothing to look at, there is nothing to render.

The real world is made of objects having a very wild variety of shapes, appearances, and structures. For example, what's the difference between smoke, a chair, and water making up the ocean? In computer graphics, we generally like to see objects as either being solid or not. However, in the real world, the only thing that differentiates the two is the density of matter making up these objects. Smoke is made of molecules loosely connected and separated by a large amount of empty space, while wood making up a chair is made of molecules tightly packed into the smallest possible space. In CG though, we generally just need to define the object's external shape (we will speak about how we render non-solid objects later on in this lesson). How do we do that?

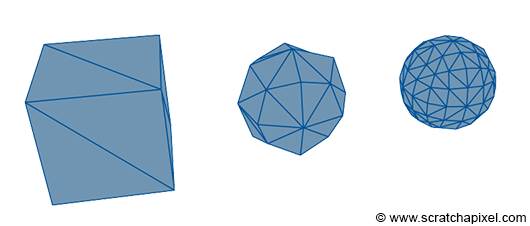
In the previous lesson, Where Do I Start? A Gentle Introduction to Computer Graphics Programming, we already introduced the idea that defining shape within the memory of a computer, we needed to start defining the concept of point in 3D space. Generally, a point is defined as three floats within the memory of a computer, one for each of the three-axis of the Cartesian coordinate system: the x-, y- and z-axis. From here, we can simply define several points in space and connect them to define a surface (a polygon). Note that polygons should always be coplanar which means that all points making up a face or polygon should lie on the same plane. With three points, you can create the simplest possible shape of all: a triangle. You will see triangles used everywhere especially in ray-tracing because many different techniques have been developed to efficiently compute the intersection of a line with a triangle. When faces or polygons have more than three points (also called vertices), it's not uncommon to convert these faces into triangles, a process called triangulation.

We will explain later in this lesson, why converting geometry to triangles is a good idea. But the point here is that the simplest possible surface or object you can create is a triangle, and while a triangle on its own is not very useful, you can though create more complex shapes by assembling triangles. In many ways, this is what modeling is about. The process is very similar to putting bricks together to create more complex shapes and surfaces.

The world is not polygonal!

Most people new to computer graphics often ask though, how can curved surfaces be created from triangles, when a triangle is a flat and angular surface. First, the way we define the surface of objects in CG (using triangles or polygons) is a very crude representation of reality. What may seem like a flat surface (for example the surface of a wall) to our eyes, is generally an incredibly complex landscape at the microscopic level. Interestingly enough, the microscopic structure of objects has a great influence on their appearance, not on their overall shape. Something worth keeping in mind. But to come back to the main question, using triangles or polygons is indeed not the best way of representing curved surfaces. It gives a faceted look to objects, a little bit like a cut diamond (this facet look can be slightly improved with a technique called smooth shading, but smooth shading is just a trick we will learn about when we go to the lessons on shading). If you draw a smooth curve, you can approximate this curve by placing a few points along this curve and connecting these points with straight lines (which we call segments). To improve this approximation you can simply reduce the size of the segment (make them smaller) which is the same as creating more points along the curve. The process of actually placing points or vertices along a smooth surface is called sampling (the process of converting a smooth surface to a triangle mesh is called tessellation. We will explain further in this chapter how smooth surfaces can be defined). Similarly, with 3D shapes, we can create more and smaller triangles to better approximate curved surfaces. Of course, the more geometry (or triangles) we create, the longer it will take to render this object. This is why the art of rendering is often to find a tradeoff between the amount of geometry you use to approximate the curvature of an object and the time it takes to render this 3D model. The amount of geometric detail you put in a 3D model also depends on how close you will see this model in your image. The closer you are to the object, the more details you may want to see. Dealing with model complexity is also a very large field of research in computer graphics (a lot of research has been done to find automatic/adaptive ways of adjusting the number of triangles an object is made of depending on its distance to the camera or the curvature of the object).

Polygonal meshes are easy which is why they are popular (most objects you see in CG feature films or video games are defined that way: as an assembly of polygons or triangles) however as suggested before, they are not great to model curved or organic surfaces. This became a particular issue when computers started to be used to design manufactured objects such as cars (CAD). NURBS or Subdivision surfaces were designed to address this particular shortcoming. They are based on the idea that points only define a control mesh from which a perfect curved surface can be computed mathematically. The surface itself is purely the result of an equation thus it can not be rendered directly (nor is the control mesh which is only used as an input to the algorithm). It needs to be sampled, similarly to the way we sampled the curve earlier on (the points forming the base or input mesh are usually called control points. One of the characteristics of these techniques is that the resulting surface, in general, does not pass through these control points). The main advantage of this approach is that you need fewer points (fewer compared to the number of points required to get a smooth surface with polygons) to control the shape of a perfectly smooth surface, which can then be converted to a triangular mesh smoother than the original input control mesh. While it is possible to create curved surfaces with polygons, editing them is far more time-consuming (and still less accurate) than when similar shapes can be defined with just a few points as with NURBS and Subdivision surfaces. If they are superior, why are they not used everywhere? They almost are. They are (slightly) more expansive to render than polygonal meshes because a polygonal mesh needs to be generated from the control mesh first (it takes an extra step), which is why they are not always used in video games (but many game engines such as the Cry Engine implement them), but they are in films. NURBS are slightly more difficult to manipulate overall than polygonal meshes. This is why artists generally use subdivision surfaces instead, but they are still used in design and CAD, where a high degree of precision is needed. Nurbs and Subdivisions surfaces will be studied in the Geometry section, however, in a further lesson in this section, we will learn about Bezier curves and surfaces (to render the Utah teapot), which in a way, are quite similar to NURBS.

In most cases, 3D models are generated by hand. By hand, we mean that someone creates vertices in 3D space and connects them to make up the faces of the object. However, it is also possible to use simulation software to generate geometry. This is generally how you create water, smoke, or fire. Special programs simulate the way fluids move and generate a polygon mesh from this simulation. In the case of smoke or fire, the program will not generate a surface but a 3D dimensional grid (a rectangle or a box that is divided into equally spaced cells also called voxels). Each cell of this grid can be seen as a small volume of space that is either empty or occupied by smoke. Smoke is mostly defined by its density which is the information we will store in the cell. Density is just a float, but since we deal with a 3D grid, a 512x512x512 grid already consumes about 512Mb of memory (and we may need to store more data than just density such as the smoke or fire temperature, its color, etc.). The size of this grid is 8 times larger each time we double the grid resolution (a 1024x1024x1024 requires 4Gb of storage). Fluid simulation is computationally intensive, the simulation generates very large files, and rendering the volume itself generally takes more time than rendering solid objects (we need to use a special algorithm known as ray-marching which we will briefly introduce in the next chapters). In the image above (figure 6), you can see a screenshot of a 3D grid created in Maya.

When ray tracing is used, it is not always necessary to convert an object into a polygonal representation to render it. Ray tracing requires computing the intersection of rays (which are simply lines) with the geometry making up the scene. Finding if a line (a ray) intersects a geometrical shape, can sometimes be done mathematically. This is either possible because:

• a geometric solution or,

• an algebraic solution exists to the ray-object intersection test. This is generally possible when the shape of the object can be defined mathematically, with an equation. More generally, you can see this equation, as a function representing a surface (such as the surface of a sphere) overall space. These surfaces are called implicit surfaces (or algebraic surfaces) because they are defined implicitly, by a function. The principle is very simple. Imagine you have two equations:

  $$ \begin{array}{l} y = 2x + 2\\ y = -2x.\\ \end{array} $$

  

  You can see a plot of these two equations in the adjacent image. This is an example of a system of linear equations. If you want to find out if the two lines defined by these equations meet in one point (which you can see as an intersection), then they must have one x for which the two equations give the same y. Which you can write as:

  $$ 2x + 2 = -2x. $$

  Solving for x, you get:

  $$ \begin{array}{l} 4x + 2 = 0\\ 4x = -2\\ x = -\dfrac{1}{2}\\ \end{array} $$

  Because a ray can also be defined with an equation, the two equations, the equation of the ray and the equation defining the shape of the object, can be solved like any other system of linear equations. If a solution to this system of linear equations exists, then the ray intersects the object.

A very good and simple example of a shape whose intersection with a ray can be found using the geometric and algebraic method is a sphere. You can find both methods explained in the lesson Rendering Simple Shapes.

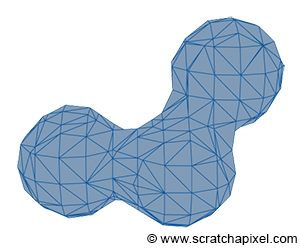
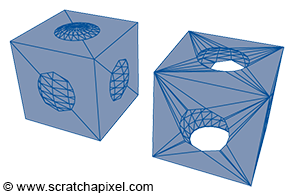
Implicit surfaces are very useful in modeling but are not very common (and certainly less common than they used to be). It is possible to use implicit surfaces to create more complex shapes (implicit primitives such as spheres, cubes, cones, etc. are combined through boolean operations), a technique called constructive solid geometry (or CSG). Metaballs (invented in the early 1980s by Jim Blinn) is another form of implicit geometry used to create organic shapes.

The problem though with implicit surfaces is that they are not easy to render. While it's often possible to ray trace them directly (we can compute the intersection of a ray with an implicit surface using an algebraic approach, as explained earlier), they first need to be converted to a mesh otherwise. The process of converting an implicit surface to a mesh is not as straightforward as with NURBS or Subdivision surface and requires a special algorithm such as the marching cube algorithm (proposed by Lorensen and Cline in 1987). It can also potentially lead to creating heavy meshes.

Check the section on Geometry, to read about these different topics in detail.

Triangle as the Rendering Primitive

In this series of lessons, we will study an example of an implicit surface with the ray-sphere intersection test. We will also see an example of a parametric surface, with the Utah teapot, which is using Bezier surfaces. However, in general, most rendering APIs choose the solution of actually converting the different geometry types to a triangular mesh and render the triangular mesh instead. This has several advantages. Supporting several geometry types such as polygonal meshes, implicitly or parametric surfaces requires writing a ray-object routine for each supported surface type. This is not only more code to write (with the obvious disadvantages it may have), but it is also difficult if you make this choice, to make these routines work in a general framework, which often results in downgrading the performance of the render engine.

Keep in mind that rendering is more than just rendering 3D objects. It also needs to support many features such as motion blur, displacement, etc. Having to support many different geometry surfaces, means that each one of these surfaces needs to work with the entire set of supported features, which is much harder than if all surfaces are converted to the same rendering primitive, and if we make all the features work for this one single primitive only.

You also generally get better performances if you limit your code to rendering one primitive only because you can focus all your efforts to render this one single primitive very efficiently. Triangles have generally been the preferred choice for ray tracing. A lot of research has been done in finding the best possible (fastest/least instructions, least memory usage, and most stable) algorithm to compute the intersection of a ray with a triangle. However, other rendering APIs such as OpenGL also render triangles and triangles only, even though they don't use the ray tracing algorithm. Modern GPUs in general, are designed and optimized to perform a single type of rendering based on triangles. Someone (humorously) wrote on this topic:

Because current GPUs are designed to work with triangles, people use triangles and so GPUs only need to process triangles, and so they're designed to process only triangles.

Limiting yourself to rendering one primitive only, allows you to build common operations directly into the hardware (you can build a component that is extremely good at performing these operations). Generally, triangles are nice to work with for plenty of reasons (including those we already mentioned). They are always coplanar, they are easy to subdivide into smaller triangles yet they are indivisible. The maths to interpolate texture coordinates across a triangle are also simple (something we will be using later to apply a texture to the geometry). This doesn't mean that a GPU could not be designed to render any other kind of primitives efficiently (such as quads).

A 3D Scene Is More Than Just Geometry

Typically though a 3D scene is more than just geometry. While geometry is the most important element of the scene, you also need a camera to look at the scene itself. Thus generally, a scene description also includes a camera. And a scene without any light would be black, thus a scene also needs lights. In rendering, all this information (the description of the geometry, the camera, and the lights) is contained within a file called the scene file. The content of the 3D scene can also be loaded into the memory of a 3D package such as Maya or Blender. In this case, when a user clicks on the render button, a special program or plugin will go through each object contained in the scene, each light, and export the whole lot (including the camera) directly to the renderer. Finally, you will also need to provide the renderer with some extra information such as the resolution of the final image, etc. These are usually called global render settings or options.

Summary

What you should remember from this chapter is that we first need to consider what a scene is made of before considering the next step, which is to create an image of that 3D scene. A scene needs to contain three things: geometry (one or several 3D objects to look at), lights (without which the scene will be black), and a camera, to define the point of view from which the scene will be rendered. While many different techniques can be used to describe geometry (polygonal meshes, NURBS, subdivision surfaces, implicit surfaces, etc.) and while each one of these types may be rendered directly using the appropriate algorithm, it is easier and more efficient to only support one rendering primitive. In ray tracing and on modern GPUs, the preferred rendering primitive is the triangle. Thus, generally, geometry will be converted to triangular meshes before the scene gets rendered.