Rendering an Image of a 3D Scene

It All Starts with a Computer and a Computer Screen

Introduction

The lesson Introduction to Raytracing: A Simple Method for Creating 3D Images offered a brief overview of key concepts in rendering and computer graphics, alongside the source code for a simple ray tracer that rendered a scene with a few spheres. Ray tracing is a highly favored technique for rendering 3D scenes, primarily because it is intuitively easy to implement and naturally mimics how light propagates in space, as briefly explained in the first lesson. However, other methods exist. This lesson will delve into what rendering entails, the challenges involved in producing an image of a 3D scene, and a quick review of the most significant techniques developed to address these challenges, focusing on ray tracing and rasterization methods, two popular algorithms for solving the visibility problem (determining which objects in the scene are visible through the camera). We will also explore shading, which defines the appearance and brightness of objects.

It All Starts with a Computer (and a Computer Screen)

The journey into computer graphics begins with... a computer. It may seem obvious, but it's so fundamental that it's often taken for granted without considering its implications for creating images with a computer. More than a computer, we should focus on how images are displayed: the computer screen. Both the computer and the screen share a critical characteristic: they operate with discrete structures, unlike the continuous structures that compose the world around us (at least at the macroscopic level). These discrete structures are the bit for the computer and the pixel for the screen. Consider a thread in the real world—it is indivisible. However, representing this thread on a computer screen requires "cutting" or "breaking" it down into small pieces, known as pixels. This concept is illustrated in Figure 1.

In computing, the act of converting any continuous object (a continuous function in mathematics, a digital image of a thread) is called discretization. Obvious? Yes, and yet, most, if not all, problems in computer graphics stem from the very nature of the technology a computer is based on: 0s, 1s, and pixels.

You might wonder, "Who cares?" For someone watching a video on a computer, it's probably not very important. But if you're creating that video, it becomes a crucial consideration. Imagine needing to represent a sphere on a computer screen. We apply a grid on the sphere, symbolizing the pixels of your screen (Figure 2). Some pixels are fully overlapped by the sphere, while others are empty. However, some pixels face a dilemma—the sphere only partially overlaps them. In such cases, should we fill the pixel with the background color or the object color?

Intuitively, you might think, "If the background occupies 35% of the pixel area, and the object 65%, let's assign a color to the pixel composed of 35% background color and 65% object color." This logic is sound, but it merely shifts the problem. How do we compute these areas in the first place? One solution is to subdivide the pixel into sub-pixels, count the number of sub-pixels overlapped by the background, and assume the rest are overlapped by the object. The background's area can then be calculated by taking the number of sub-pixels overlapped by the background over the total number of sub-pixels.

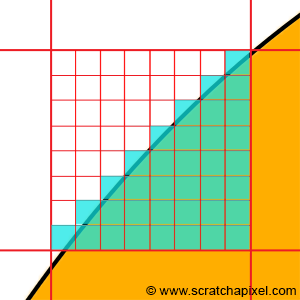
However, no matter how small the sub-pixels are, there will always be some of them overlapping both the background and the object. While you might get a pretty good approximation of the object and background coverage that way (the smaller the sub-pixels, the better the approximation), it will always just be an approximation. Computers can only approximate. Different techniques can be used to compute this approximation (subdividing the pixel into sub-pixels is just one of them). But what we need to remember from this example is that many problems we will have to solve in computer science and computer graphics come from having to "simulate" the world, which is made of continuous structures, with discrete structures. And having to go from one to the other raises all sorts of complex problems (or maybe simple in their comprehension, but complex in their resolution).

Another way of solving this problem is, obviously, to increase the resolution of the image. In other words, to represent the same shape (the sphere) using more pixels. However, even then, we are limited by the screen's resolution.

Images and screens that use a two-dimensional array of pixels to represent or display images are called raster graphics and raster displays, respectively. The term raster more generally defines a grid of x and y coordinates on a display space. We will learn more about rasterization in the chapter on perspective projection.

As suggested, the main issue with representing images of objects with a computer is that the object shapes need to be "broken" down into discrete surfaces, the pixels. Computers, more generally, can only deal with discrete data. But more importantly, the definition with which numbers can be defined in the memory of the computer is limited by the number of bits used to encode these numbers. For example, the number of colors that you can display on a screen is limited by the number of bits used to encode RGB values. In the early days of computers, a single bit was used to encode the "brightness" of pixels on the screen. When the bit had the value 0, the pixel was black, and when it was 1, the pixel would be white. The first generation of computers with color displays encoded color using a single byte or 8 bits. With 8 bits (3 bits for the red channel, 3 bits for the green channel, and 2 bits for the blue channel), you can only define 256 distinct colors (2^3 * 2^3 * 2^2). What happens then when you want to display a color that is not one of the colors you can use? The solution is to find the closest possible matching color from the palette to the color you ideally want to display and display this matching color instead. This process is called color quantization.

The problem with color quantization is that when we don't have enough colors to accurately sample a continuous gradation of color tones, continuous gradients appear as a series of discrete steps or bands of color. This effect is called banding (it's also known under the term posterization or false contouring).

There's no need to worry about banding so much these days (the most common image formats use 32 bits to encode colors. With 32 bits, you can display about 16 million distinct colors). However, keep in mind that fundamentally, colors, and pretty much any other continuous function that we may need to represent in the memory of a computer, have to be broken down into a series of discrete or single quantum values, for which precision is limited by the number of bits used to encode these values.

Finally, having to break down a continuous function into discrete values may lead to what's known in signal processing and computer graphics as aliasing. The main problem with digital images is that the amount of details you can capture depends on the image resolution. The main issue with this is that small details (roughly speaking, details smaller than a pixel) can't be captured by the image accurately. Imagine, for example, that you want to take a photograph with a digital camera of a teapot that is so far away that the object is smaller than a pixel in the image (Figure 6). A pixel is a discrete structure, thus we can only fill it up with a constant color. If in this example, we fill it up with the teapot's color (assuming the teapot has a constant color, which is probably not the case if it's shaded), your teapot will only show up as a dot in the image: you failed to capture the teapot's shape (and shading). In reality, aliasing is far more complex than that, but you should know about the term and keep in mind that by the very nature of digital images (because pixels are discrete elements), an image of a given resolution can only accurately represent objects of a given size. We will explain the relationship between the objects' size and the image resolution in the lesson on Aliasing (which you can find in the Mathematics and Physics of Computer Graphics section).

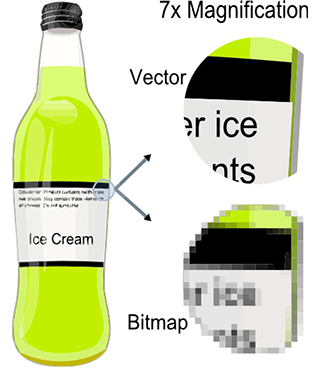
Images are just a collection of pixels. As mentioned before, when an image of the real world is stored in a digital image, shapes are broken down into discrete structures, the pixels. The main drawback of raster images (and raster screens) is that the resolution of the images we can store or display is limited by the image or the screen resolution (its dimension in pixels). Zooming in doesn't reveal more details in the image. Vector graphics were designed to address this issue. With vector graphics, you do not store pixels but represent the shape of objects (and their colors) using mathematical expressions. That way, rather than being limited by the image resolution, the shapes defined in the file can be rendered on the fly at the desired resolution, producing an image of the object's shapes that is always perfectly sharp.

To summarize, computers work with quantum values when in fact, processes from the real world that we want to simulate with computers, are generally (if not always) continuous (at least at the macroscopic and even microscopic scale). And in fact, this is a very fundamental issue that is causing all sorts of very puzzling problems, to which a very large chunk of computer graphics research and theory is devoted.