Disk and Spherical Area Light
Reading time: 27 mins.WIP. This lesson is currently being written (June 2024)
Preamble
Because each shape that an area light can have has its own specific implementation considerations, we have decided to dedicate one page per area light shape. More specifically, we will consider triangular, planar, disk, and finally spherical area lights. This preamble is repeated on each page to ensure that if you landed on one of these pages from an external link, you are aware that it is advisable to start by reading the page on the triangular area light. There, we will discuss some concepts that will be reused across the other light types and provide a general explanation about the code we will be using to implement these lights.
Also note that we strongly recommend that you read the lessons on Distributed Ray-Tracing and Stochastic Sampling and Sampling Strategies, which are corollaries to this one.
What Will You Learn in this Chapter?
As mentioned in the chapter on triangular area lights, unlike the chapter on quad lights which wasn't very different from triangular lights, implementing spherical area lights will give us an opportunity to delve into a different method of evaluating the contribution of area lights called cone sampling. Therefore, we strongly encourage you to read this chapter as carefully as you did the lesson on triangular area lights, as key concepts will be introduced here.
This chapter is divided into two main parts:
-
Implementing Spherical Area Lights Using Area Sampling: In the first part, we will learn how to implement spherical area lights using the area sampling method, which we have studied in the last two chapters. Although we will learn new critical aspects of the ray-tracing method in this section, read it carefully even if you feel familiar with the concepts from the previous chapters.
-
Learning About Cone Sampling: The second part is devoted to learning about cone sampling, another method that can be used to sample area lights.
Uniform Sampling of a Spherical Light
Similarly to how we've implemented the triangular area light, implementing spherical area lights using the area sampling method requires finding a way to sample spheres.
For the purposes of debugging, a constant density function is useful. (Peter Shirley, Changyaw Wang - Monte Carlo Techniques for Direct Lighting Calculations).
The quote above is from Peter Shirley and Changyaw Wang in their paper entitled "Monte Carlo Techniques for Direct Lighting Calculations" (see the references section at the bottom of the page). This simply means that the most basic way of sampling a spherical light is by using a uniform distribution, similar to how we sampled quad and triangular lights. This involves starting with a sample uniformly distributed on the unit square, mapping it to the sphere, and using a probability density function (PDF), which in this case is \( \frac{1}{\text{area}} \). As we know, the area of a sphere is \( 4\pi r^2 \). So far, this seems rather simple.
As with the naive method that we started with for uniformly sampling a triangle, we can ask ourselves: how would you map that sample on the unit square to the sphere?
The first thing we need to do is define a Cartesian coordinate system and a convention to define the position of a point on the sphere using spherical coordinates. When it comes to both Cartesian and spherical coordinate systems, you might come across different conventions. Here is the definition of the conventions we will be using in this chapter:
-
Cartesian Coordinate System: While this is not our preferred convention, we decided to use it. Most papers written in the 90s (or earlier) related to sampling shapes such as spheres use these conventions, and because of that historical background, many people, particularly those with a background in mathematics, keep using it today. So while this is not our preferred convention, to stay consistent with the papers we will reference at the bottom of the page, we will stick to this. In this convention, \(z\) is up, the \(x\)-axis of the Cartesian coordinate system points to the left, and the \(y\)-axis points away from you (or from the screen, as shown in Figure 1).
-
Spherical Coordinates: The papers we've been alluding to also use a convention that is the opposite of what we tend to use on the website. Let's just say that this is a good mental exercise. For the sake of this lesson, the angle \(\phi\) (Greek letter phi) will refer to the azimuthal (longitude) angle and will vary from 0 to \(2\pi\). The angle \(\theta\) (Greek letter theta) will be the polar (latitude) angle and will vary from 0 to \(\pi\). Note that the positive \(z\)-axis is \(\theta = 0\) and the positive \(x\)-axis is \(\phi = 0\).
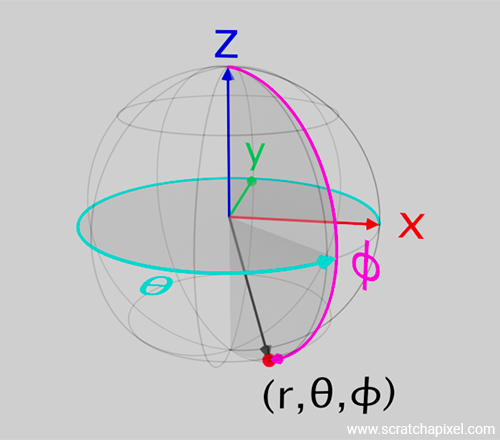
With these conventions set, here are the equations that we will be using to convert a point in spherical coordinates to Cartesian coordinates (again, refer to Figure 1):
$$ \begin{align*} x &= \cos(\theta) \sin(\phi) \\ y &= \sin(\theta) \sin(\phi) \\ z &= \cos(\phi) \end{align*} $$
Vec3 SampleUnitSphereNaive(float r1, float r2) {
float theta = 2 * M_PI * r1; // azimuthal angle
float phi = M_PI * r2; // polar angle
return {
std::cos(theta) * std::sin(phi),
std::sin(theta) * std::sin(phi),
std::cos(phi) };
}

What follows may seem a bit boring and verbose. However, it covers one of the key geometrical constructs in 3D graphics. The bottom line is that the following content is something you will encounter repeatedly in CG-related papers and resources. If you make the effort to thoroughly understand this content—not just memorize it—it will save you a lot of time in the future.
The result visible in Figure 2 clearly shows that with this approach, there is a concentration of samples near the poles. We will explain shortly why this is happening, but in a broader scope, the reason is similar to the problem of remapping samples on the unit square to the triangle. We spoke about the Jacobian being the scale factor applied when you transform one "shape" (the unit square) to another (the triangle). For the uniform distribution property to remain uniform after transformation, the Jacobian needs to be constant. The issue with the way we are remapping the samples from the unit square to the sphere using this basic approach is precisely that the Jacobian is not constant. One way to understand this is to consider a small differential area on the sphere parameterized in terms of spherical coordinates. Let's look at the equation and break it down:
$$dA = r^2 \sin(\phi) \, d\theta \, d\phi$$where \(r\) in the above equation stands for the sphere's radius. The idea is to take a small differential angle in both \(\theta\) and \(\phi\), which, when multiplied by each other, would give you the area of a small patch on the surface of the sphere. You can see a representation of this small differential area and the terms used to calculate it in the following figure:
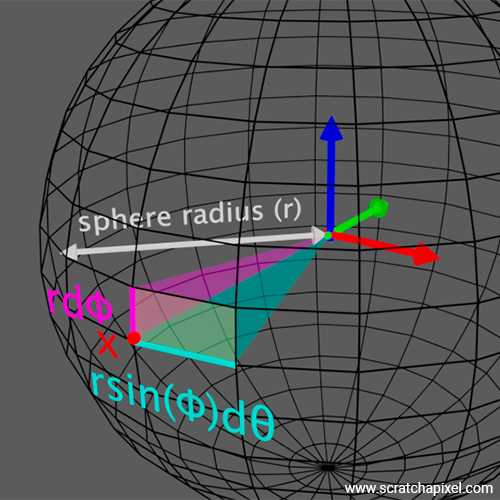
Basically, if you imagine that we want to determine a small differential area at point \(x\) on the sphere as shown in the figure. It doesn't matter if \(x\) is centered with respect to that small differential area (the transparent yellow patch in Figure 3) or to the side of it as represented in Figure 3. The concept is the same regardless. Now, the position of \(x\) on the sphere in terms of spherical coordinates is \(\theta\) (azimuthal) and \(\phi\) (polar). The sphere has a radius \(r\). So from \(x\), we move up by a tiny fraction \(\phi\), hence the \(d\phi\) multiplied by the sphere radius. In the end, this gives us \(\textcolor{magenta}{r d\phi}\). And we do the same thing with \(\theta\), so technically we could write \(r d\theta\). However, note that for any given \(d\theta\), the length of the given horizontal segment (the segment highlighted with the cyan color in the figure) varies with \(\phi\). The closer we are to the pole, the smaller the segment; the closer we are to the equator, the larger the segment. This can be seen in the following figure, which gives a view of the sphere rendered from the top, where from the sphere, we've only represented three of such possible longitudinal lines. Within a given small differential angle for \(\theta\), we can see that the segment along the sphere equator is larger than those that are close to the pole.
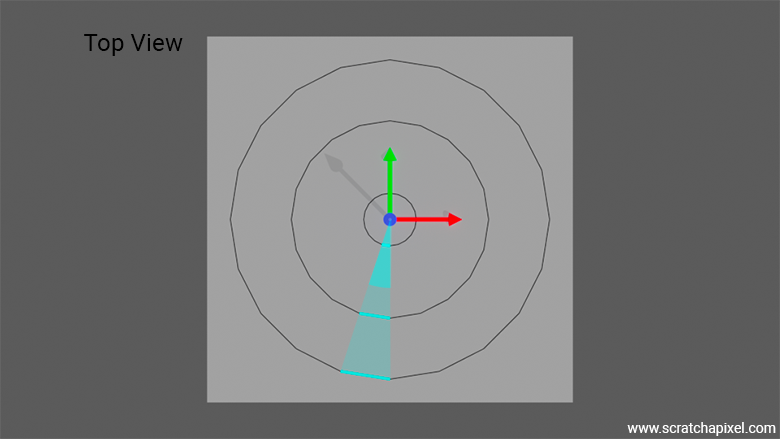
The length of these segments is proportional to the radius of the sphere where these segments are being created, and this radius is given by \(r \sin(\phi)\). This can be more easily understood if you look at the following figure, in which we show that the inner circle (in grey) has a radius \(r \sin(\phi)\), from which we can see that the segment length is \(\textcolor{cyan}{r \sin(\phi) d\theta}\).

The area of the small differential area being the product of these two segments (the one we got by moving along \(\phi\) and the one we got by moving along \(\theta\)) is indeed \(dA = \textcolor{cyan}{r \sin(\phi) d\theta} \, \textcolor{magenta}{r d\phi} = r^2 \textcolor{cyan}{\sin(\phi) d\theta}\textcolor{magenta}{d\phi}\).
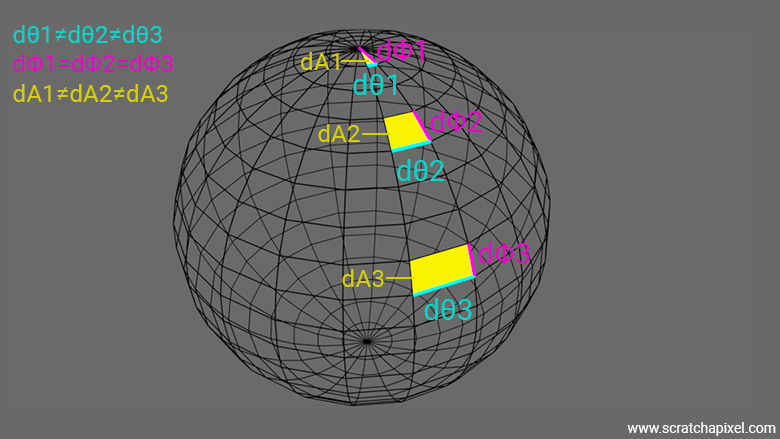
As a consequence of this, you can easily see by looking at the following figure that differential areas near the pole are much smaller than those near the sphere's equator. This explains why our remapping process doesn't work. The process we've been using to transform the unit square to a sphere doesn't preserve area (the Jacobian is not constant). Therefore, as the area gets squeezed towards the poles, we get a concentration of samples in these regions.
If the equation for a small differential area on the sphere \( dA = r^2 \sin(\phi) \, d\phi \, d\theta \) is correct, then its integration over the domain of \(\theta\) and \(\phi\), which are \(0\) to \(2\pi\) and \(0\) to \(\pi\) respectively, should give us the area of the sphere (if you cover the sphere with post-its and know the area of a given post-it, the number of post-its that you used to cover the sphere multiplied by the post-it area should give you the area of the sphere), which is \(4\pi r^2\). Let's see.
Let's first look at the integral over \(\phi\):
$$ \int_{0}^{\pi} r^2 \sin(\phi) \, d\phi $$Since \(r^2\) is a constant with respect to \(\phi\), we can factor it out:
$$ r^2 \int_{0}^{\pi} \sin(\phi) \, d\phi $$The integral of \(\sin(\phi)\) is \(-\cos(\phi)\):
$$ r^2 \left[ -\cos(\phi) \right]_{0}^{\pi} $$Evaluate the definite integral:
$$ r^2 \left[ -\cos(\pi) - (-\cos(0)) \right] $$Since \(\cos(\pi) = -1\) and \(\cos(0) = 1\):
$$ r^2 \left[ -(-1) - (-1) \right] = r^2 [1 + 1] = r^2 \cdot 2 = 2r^2 $$Now, integrate with respect to \(\theta\):
$$ \int_{0}^{2\pi} 2r^2 \, d\theta $$Again, \(2r^2\) is a constant with respect to \(\theta\), so we can factor it out:
$$ 2r^2 \int_{0}^{2\pi} \, d\theta $$The integral of \(d\theta\) with respect to \(\theta\) is \(\theta\):
$$ 2r^2 \left[ \theta \right]_{0}^{2\pi} $$Evaluate the definite integral:
$$ 2r^2 \left[ 2\pi - 0 \right] = 2r^2 \cdot 2\pi = 4\pi r^2 $$In conclusion, the surface area of a sphere is given by:
$$ \text{Area} = 4\pi r^2 $$Our equation for calculating a differential area for the sphere works.
We've learned why this doesn't work, but then can we make it work? Hopefully yes. To understand how to solve this problem, we need to delve into the theory of probabiliy which is what we are going to do next. Take your time to read the following content, as it will set some key techniques that you will come across over and over in 3D rendering.
Sampling a Non-Uniform Probabiliy Density Function: A Dive in Probability Theory
Objective: Our objective is to use two uniformly distributed random numbers, \(\varepsilon_1\) and \(\varepsilon_2\), to generate samples uniformly distributed across the surface of a sphere. The positions of these samples will be defined by their spherical coordinates \(\theta\) and \(\phi\).
The problem we face is that, intuitively, without even knowing the specifics of the function, one can easily understand that the result of sampling the sphere using a uniformly distributed pair of random numbers leads to a non-uniform distribution of samples (due to the density function \(dA\)). We have a higher concentration of samples at the poles.
Our goal is to cancel out this higher concentration of samples at the poles so that the final distribution of samples over the sphere is uniform. For that, we will need to resort to a method that was initially developed and used in the 1950s. Remember that the probability of a uniform sampling distribution of samples across the surface of the sphere is:
$$p(x) = \dfrac{1}{4\pi r^2}$$where \(x\) marks the sample, and \(p(x)\) indicates the probability of that sample being chosen (which, in this case, as we know, is uniform). The density function of the sphere parameterized in terms of \(\theta\) and \(\phi\) is:
$$dA = r^2 \sin(\phi) \, d\phi \, d\theta$$The first equation ensures equal probability per unit area over the sphere's surface. The second equation indicates how the area changes with \(\theta\) and \(\phi\). Hold on to these two descriptions. Now if we combine the two together, that is, we write:
$$ \begin{array} p(\theta, \phi) &=& \dfrac{1}{4\pi r^2} \times r^2 \sin(\phi) \, d\phi \, d\theta \\ &=& \dfrac{1}{4\pi} \times \sin(\phi) \, d\phi \, d\theta \end{array} $$This function is a valid probability density function in the sense that it can be integrated over the sphere to give 1, representing the total probability, i.e., certainty that a point lies on the sphere's surface. We showed in the note above that integrating the differential area over the range \(0 \leq \theta \leq 2\pi\) and \(0 \leq \phi \leq \pi\) results in \(4\pi r^2\). That combined density describes how the probability is distributed over the surface of the sphere in terms of the spherical coordinates \(\theta\) and \(\phi\).
Now we can look at this equation \(p(\theta, \phi)\) as being essentially made of two parts:
-
\(p(\theta) = d\theta\)
-
\(p(\phi) = \sin(\phi)d\phi\)
We've left the \(1 / 4\pi\) out of the equation (the \(r^2\) terms cancel out) because it has no effect on the distribution of \(\theta\) and \(\phi\) respectively. We are only interested in the terms that directly relate to these two parameters which are \(\theta\) and \(\phi\).
These densities are expressed with their differential elements. The term \(d\theta\) suggests that \(\theta\) is uniformly distributed over its domain \([0, 2\pi]\). The term \(\sin(\phi) d\phi\) suggests a non-uniform distribution over \([0, \pi]\). We need to integrate them over their respective domains \([0, 2\pi]\) and \([0, \pi]\) to handle normalization. Normalization ensures that the total probability over the entire space sums to 1. Without normalization, the probability densities might not integrate to 1, leading to an incorrect representation of the distribution (this will make more sense very soon).
Let's first integrate \(p(\theta)\):
$$\int_0^{2\pi} d\theta = 2\pi$$Therefore, \(p(\theta) = \dfrac{1}{2\pi}\). Now let's go through the same process for \(\phi\). Let's integrate its differential form:
$$\int_0^\pi \sin(\phi) \, d\phi = [-\cos(\phi)]_0^\pi = -\cos(\pi) - (-\cos(0)) = -(-1) - (-1) = 2$$Therefore, \(p(\phi) = \dfrac{\sin(\phi)}{2} \).
It's important to understand that \(\textcolor{cyan}{p(\theta) = d\theta}\) and \(\textcolor{cyan}{p(\theta) = {1}/{2\pi}}\) or \(\textcolor{magenta}{p(\phi) = \sin(\phi) d\phi}\) and \(\textcolor{magenta}{p(\phi) = {\sin(\phi)}/{2}}\) are effectively the same functions. The first form is the differential form of the second (the normalized version; see below). They describe how the probability density is distributed over the infinitesimal element \(d\theta\) (or \(d\phi\)). When integrating these differential equations over their domain, we might get a number different from 1. However, to use these functions as probability functions, their integration over the domain needs to sum to 1 (the sum of probabilities is required to be 1). Thus, multiplying the differential form of these equations by the reciprocal of the result of the integration gives us a function that will integrate to 1 (hence the need for the normalization step). Let's verify:
-
For \(\theta\): \(\frac{1}{2\pi} \int_0^{2\pi} \, d\theta = \frac{1}{2\pi} \times 2\pi = 1\).
-
For \(\phi\): \(\frac{1}{2} \int_0^\pi \sin(\phi) \, d\phi = \frac{1}{2} \int_0^\pi \sin(\phi) \, d\phi = \frac{1}{2} \times 2 = 1\).
Where \(1/2\pi\) and \(1/2\) are the normalizing factors for \(p(\theta)\) and \(p(\phi)\) respectively.
It's really important to understand this part. If we haven't explained it clearly enough, please let us know, and we will try to rephrase it until you understand.
The reason why we've separated these two functions in the first place is because, in this particular case:
$$p(\theta, \phi) = p(\theta) \times p(\phi)$$So, the probability of drawing a sample with spherical coordinates \(\theta\) and \(\phi\) (where both of these numbers are random variables) is equal to the product of the probability of drawing \(\theta\) and the probability of drawing \(\phi\). In mathematics (and probability theory), this is called a joint probability and \(p(\theta)\) and \(p(\phi)\) are called marginal probabilities (or distributions). We said "in this particular case" because \(\theta\) and \(\phi\) are independent variables (in this particular case). This technique couldn't be used if these random variables were not independent.
\(\theta\) and \(\phi\) are independent if knowing the value of one does not provide any information about the value of the other. In other words, the way \(\theta\) is distributed does not affect the way \(\phi\) is distributed, and vice versa.
Remember what our objective is: we can generate random numbers uniformly sampled in the range [0,1], and we want to use them to come up with values for \(\theta\) and \(\phi\) in such a way that the resulting samples will be uniformly distributed across the surface of a sphere. Remember also that the PDF provides the likelihood of a random variable taking the value \(x\). The PDF describes a density of probability or how densely the probability mass is distributed at each point in the domain.
There's another useful function in probability theory called the cumulative density function or CDF, which can be built from the PDF. We will explain how in a moment, but for now, we will first understand what the CDF is. Assuming you have a CDF, \(F(x)\), defined as:
$$F(x) = P(X \le x)$$This function gives the probability that a random variable \(X\) is less than or equal to \(x\). To be clear, you somehow draw a random number, say 5, and you want to know the probability that any of the possible dice outcomes will be lower or equal to 5. The \(X\) are the numbers on the dice (all the possible outcomes), which is a random variable since each time you throw the dice, you get a different number. You draw another random number, 5, that's your \(x\), and you want to know the probability that you get a number lower or equal to 5 when you throw the dice on the table. If you are comfortable with that example, which is rather simple, you might have already guessed that this probability is the sum of the probabilities of getting a 1, a 2, a 3, a 4, or a 5. That is 5 times \(1/6\), which is \(5/6\). This example uses discrete random variables, but for a continuous one, we can formalize this by writing that the CDF of a probability density function is the integral (what the sum is to discrete random variables is the integral to continuous variables) of the probability density function (the probability of the random variable \(X\) from whatever is the base range of that random variable (we assume minus infinity here, but for a dice example, if this had been a continuous function, it would have been 1) to whatever value you are interested in (again, if the dice example had been a continuous function, this would have been our 5).
$$F(x) = P(X \le x) = \int_{-\infty}^{x} p(t)dt$$While this can be a bit abstract at first, let's give an example. Imagine we have the following PDF: \(\lambda e^{-\lambda x}\). This PDF integrates to 1, and the proof of that is given in the box below if you are interested, so it can effectively be considered a valid PDF.
Let's verify mathematically that the probability density function (PDF) of the exponential distribution \(p(x) = \lambda e^{-\lambda x}\) integrates to 1 over its domain, which is from 0 to \(\infty\). To integrate \(\lambda e^{-\lambda x}\), we perform the following steps:
-
Factor out the constant \(\lambda\):
$$ \int_0^\infty \lambda e^{-\lambda x} \, dx = \lambda \int_0^\infty e^{-\lambda x} \, dx $$ -
Substitute \(u = \lambda x\) (where \(du = \lambda dx\) or \(dx = \frac{du}{\lambda}\)):
$$ \lambda \int_0^\infty e^{-\lambda x} \, dx = \lambda \int_0^\infty e^{-u} \cdot \frac{du}{\lambda} $$ -
Simplify:
$$ \lambda \int_0^\infty e^{-u} \cdot \frac{du}{\lambda} = \int_0^\infty e^{-u} \, du $$ -
Integrate:
$$ \int_0^\infty e^{-u} \, du = \left[ -e^{-u} \right]_0^\infty $$ -
Evaluate the definite integral:
$$ \left[ -e^{-u} \right]_0^\infty = \left( 0 - (-1) \right) = 1 $$
Therefore: \(\int_0^\infty \lambda e^{-\lambda x} \, dx = 1\). This confirms that the PDF of the exponential distribution integrates to 1, as required for any valid probability density function.
To keep things simple, we will write a simple program that helps plot both the PDF and the CDF for the range [0,5]. To do so, we will evaluate the PDF for small steps of \(x\) going from 0 to 5, and for each step, set the CDF as the sum of all the PDFs we have calculated at the preceding steps, plus the current PDF value multiplied by the step size (the \(dt\) in the equation \(\int_{-\infty}^{x} p(t)dt\), see below).
#include <stdio.h>
#include <math.h>
double pdf(double x, double lambda) {
return lambda * exp(-lambda * x);
}
int main() {
double lambda = 1.0; // Rate parameter
double step = 0.1; // Step size
double x, pdf_value, cdf_value = 0.0;
printf("x\tPDF\t\tCDF\n");
for (x = 0.0; x <= 5.0; x += step) {
pdf_value = pdf(x, lambda);
cdf_value += pdf_value * step; // Accumulate the CDF
printf("%0.6f\t%0.6f\t%0.6f\n", x, pdf_value, fmin(cdf_value, 1.0));
}
return 0;
}
The following image shows a plot of these two graphs: the PDF of \(p(x) = \lambda e^{-\lambda x}\) on the left, and its resulting CDF on the right.
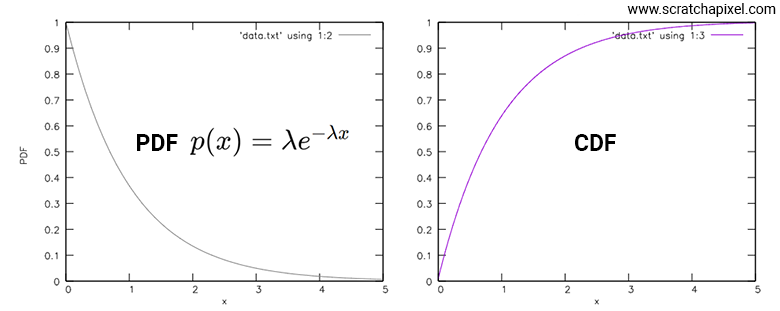
You might be surprised that the CDF doesn't start with the same value as the PDF at \(x\) because we suggested the CDF was equal to whatever its counterpart PDF at \(x\) was plus the sum of all preceding probabilities (preceding \(x\)). That works for discrete random variables, but for continuous random variables, in the integration process, you need to account for the \(dt\) term, which if you use the Riemann sum numerical method for evaluating that integral, as we did in our program, would be represented by the code's step variable. So each time you add the current CDF for the current \(x\), you need to multiply that value by step, which is why the CDF starts much lower.
That being said, what's more interesting about the CDF curve are the following points:
-
It never goes above one: Of course, since the CDF represents the probability of a number being lower than any of the outcomes a random variable \( X \) can take, the maximum value a CDF can take is necessarily in the range [0,1].
-
The curve is not linear: Naturally, it's not linear because the PDF is not linear either. Therefore, it reflects the non-linearity of the function it was derived from. More on that in a moment.
-
The curve is monotonically increasing (or non-decreasing, as some prefer to say): This property is key for various reasons, which we will discuss shortly.
With this being said, and before we explain how to exploit the above properties, let's see how this applies to our sphere-uniform-sampling problem. The equation we want the CDF of is \( p(\phi) = {\sin(\phi)}/{2} \). Let's apply the recipe to get the CDF, which involves integrating this function from the lower bound of \(\phi\) (which is 0) to some value \(\phi\).
If you are uncomfortable with how to integrate differential equation, and notably how to calcualting the integral of a function \(f\) using its antioderivative \(F\) we strongly recommand you to read the lesson on The Mathematics of Shading.
-
The given PDF is \( p(\phi) = \dfrac{\sin(\phi)}{2} \).
-
The CDF, \( F(\phi) \), is defined as the integral of the PDF from the lower bound of \(\phi\) (which is 0) to some value \(\phi\): \( F(\phi) = \int_{0}^{\phi} \dfrac{\sin(\phi')}{2} \, d\phi' \).
-
To find the CDF, we need to integrate the PDF: \( F(\phi) = \int_{0}^{\phi} \dfrac{\sin(\phi')}{2} \, d\phi' \).
-
We can perform the integration step-by-step:
$$F(\phi) = \frac{1}{2} \int_{0}^{\phi} \sin(\phi') \, d\phi'$$ $$F(\phi) = \frac{1}{2} \left[ -\cos(\phi') \right]_{0}^{\phi}$$ -
Evaluate the definite integral by substituting the limits:
$$F(\phi) = \frac{1}{2} \left( -\cos(\phi) - (-\cos(0)) \right)$$Since \(\cos(0) = 1\), this simplifies to:
$$F(\phi) = \frac{1}{2} \left( -\cos(\phi) + 1 \right)$$Simplifying further, we get:
$$F(\phi) = \frac{1}{2} \left( 1 - \cos(\phi) \right)$$
The CDF for the given PDF is:
Let's plot this equation over the domain covered by \(\phi\) (0 to \(\pi\)).
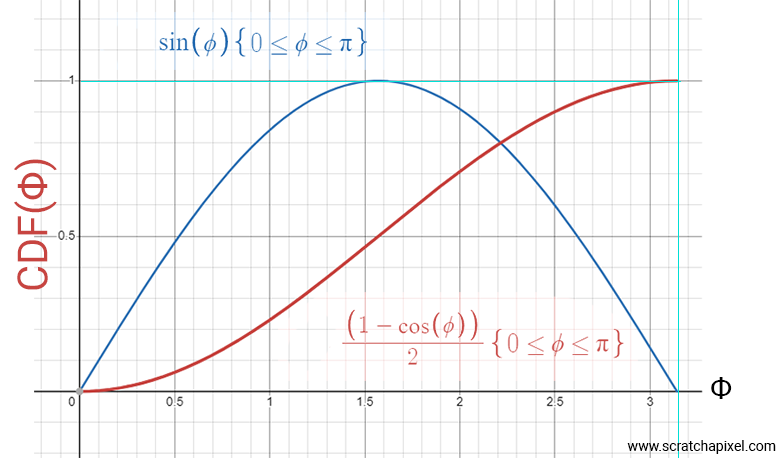
The curve we are interested in is the one in a reddish color. We've added the plot of the sine function within the same range (0 to \(\pi\)) so you can compare the two and see how the CDF relates to the original PDF. Not surprisingly, this red curve has a slower slope at the beginning and end, which is where \(\phi\) approaches the poles. A shallower slope indicates that the probability of our random variable \(X\) being in these ranges is lower than in areas where the curve is steeper. In conclusion, this CDF shows that the probability of having a random variable \(X\) around the poles is indeed lower than elsewhere on the sphere, which is what we are looking for.
Now, the reason why this CDF is wonderful is that it gives us the probability (the value on the y-axis of the plot) that a random variable \(X\) (assumed to be uniformly distributed over the surface of the sphere) has an angle \(\phi\) lower or equal to a value you pick at random (within the range 0 to \(\pi\)). Pay attention here: the value on the y-axis goes from 0 to 1, and on the x-axis from 0 to \(\pi\). The curve that maps these two conforms to the distribution of uniformly distributed samples on the sphere.
So, what do we know and what are we looking for? We know we can generate a uniformly distributed random number in the range 0 to 1. What we are looking for is a number in the range 0 to \(\pi\) such that when we map the first number to the second number (the angle \(\phi\)), the obtained angle \(\phi\) guarantees a uniform distribution of samples over the sphere. Bingo! What we need is not the CDF \(F(x)\) but its inverse function, \(F^{-1}(x)\), which takes a uniformly distributed random number in the range [0,1] and gives us a value for \(\phi\).
Wow, isn't that cool? We generate a number from 0 to 1 with a uniform distribution, feed it into the inverse of the CDF \(F^{-1}(x)\), and get as a result an angle \(\phi\). Combined with the sample angle \(\theta\), this gives us a sample that is uniformly distributed over the sphere. This works because the CDF, derived from the PDF by integrating it over the function's domain, ensures that the probability distribution is correctly transformed. By doing so, the CDF captures the likelihood of generating samples across the entire surface of the sphere, thus maintaining the uniform distribution.
This also works because the CDF has the properties we mentioned above, particularly the monotonic increasing property. This means that when you use the inverse of the function to map a value from 0 to 1 to \(\phi\), the function has one and only one solution. This wouldn't work otherwise. The fact that the function is monotonic increasing also has a very cool benefit that we won't delve into in this lesson because it is explained in detail in the lesson Sampling Strategies. That cool property is that stratified samples remain stratified when we pass them through the \(F^{-1}(x)\) function. Stratified sampling is a noise reduction technique for the Monte Carlo method. In short, the idea consists of dividing your 0-1 range into cells (as many cells as needed samples) and jittering the sample within these cells. By doing so, your samples get stratified as shown in the figure below. Stratified input samples remain stratified when mapped to \(\phi\) using the inverse of the CDF, which is a property we want our remapping method to have. If this wasn't the case, we would lose the benefit of stratified sampling, effectively increasing, rather than reducing, the noise we would get from using Monte Carlo integration. This is why using the inverse of the CDF is such a cool and powerful method.
Here are the steps for inverting the CDF in the case of sphere sampling:
$$ \begin{array}{c} \varepsilon = \dfrac{(1-\cos(\phi))}{2} \\ \cos(\phi) = 1 - 2\varepsilon \\ \phi = \cos^{-1}(1 - 2\varepsilon) \\ \end{array} $$That's it! Isn't this really, really cool? So now, all you need are two random numbers in the range [0,1], and you can sample both \(\theta\) and \(\phi\).
$$ \begin{array}{rcl} \theta &=& 2 \pi \cdot \varepsilon_1 \\ \phi &=& \cos^{-1}(1 - 2 \cdot \varepsilon_2) \end{array} $$All samples generated with this method will be uniformly distributed on the sphere. Let's implement this first by examining a distribution of samples on the sphere, and then by implementing the method for our area light sampling method.
Vec3 SampleUnitSphereGood(float r1, float r2) {
float theta = 2 * M_PI * r1; // azimuthal angle
float phi = std::acos(1 - 2 * r2); // polar angle
return {
std::cos(theta) * std::sin(phi),
std::sin(theta) * std::sin(phi),
std::cos(phi) };
}
xx insert figure
Note that when it comes to code, you can use 1 - 2 * r2 directly in place of std::cos(phi). This saves a call to std::acos and std::cos. Also, note that:
So the code can be made a bit faster with :
Vec3 SampleUnitSphereGoodAndFaster(float r1, float r2) {
float theta = 2 * M_PI * r1; // azimuthal angle
float sin_phi = 2 * std::sqrt(r2 * (1 - r2));
return {
std::cos(theta) * sin_phi,
std::sin(theta) * sin_phi,
(1 - 2 * r2) };
}
/////////////////////////
References: Peter Shirley and Kenneth Chiu. A low distortion map between disk and square. J. Graph. Tools, December 1997.
(Peter Shirley, Changyaw Wang - Monte Carlo Techniques for Direct Lighting Calculations).